Question

Two concentric circular loops, one of radius $R$ and the other of radius $2 R$, lie in the $x y$-plane with the origin as their common centre, as shown in the figure . The smaller loop carries current $I_{1}$ in the anti-clockwise direction and the larger loop carries current $I_{2}$ in the clock wise direction, with $I_{2}>2 I_{1}, \vec{B}(x, y)$ denotes the magnetic field at a point $(x, y)$ in the $x y$-plane. Which of the following statement (s) is ( are ) correct?

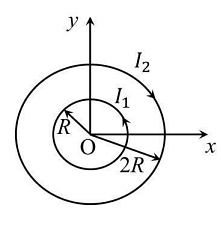
• A. $\vec{ B }( x , y )$ is perpendicular to the $xy$-plane at any point in the plane
• B. $|\vec{ B }( x , y )|$ depends on $x$ and $y$ only through the radial distance $r =\sqrt{ x ^{2}+ y ^{2}}$
• C. $|\vec{ B }( x , y )|$ is non-zero at all points for $r < R$
• D. $\vec{ B }( x , y )$ points normally outward from the $xy$-plane for all the points between the two loops

Answer 1

The Correct Option is A, B

The magnetic field generated by a circular loop is perpendicular to the plane of the loop at any point within it. Because of the loop's symmetry, the magnetic field strength solely relies on the distance from its center. Inside and outside the loop, the magnetic field direction is opposite. Consequently, the magnetic field can be nonzero for distances less than the loop's radius\( (r<R)\) because the contributions from both sides of the loop are in opposing directions.