The total electric flux through a closed spherical surface of radius \( r \) enclosing an electric dipole of dipole moment \( 2aq \) is (Give \( \epsilon_0 \) = permittivity of free space)
- Zero
- \( \frac{q}{\epsilon_0} \)
- \( \frac{2q}{\epsilon_0} \)
- \( \frac{8\pi r^2 q}{\epsilon_0} \)
The Correct Option is A
Solution and Explanation
The electric flux \( \Phi_E \) through a closed surface surrounding an electric dipole is given by Gauss’s Law:
\( \Phi_E = \frac{Q_{\text{enc}}}{\epsilon_0} \) where \( Q_{\text{enc}} \) is the net charge enclosed by the surface and \( \epsilon_0 \) is the permittivity of free space.
Since an electric dipole consists of two equal and opposite charges, the total charge enclosed by the surface is zero.
Therefore, the total electric flux through the surface is also zero:\( \Phi_E = 0 \)
Top Questions on Electric Flux
- An electric field \( \vec{E} \) is given by:
\[ \vec{E} = \begin{cases} +100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x>0 \\ -100\, \hat{i} \dfrac{\text{N}}{\text{C}} & \text{for } x<0 \end{cases} \] A right circular cylinder of length \( 10\, \text{cm} \) and radius \( 2\, \text{cm} \), is placed such that its axis coincides with the x-axis and its two faces are at \( x = -5\, \text{cm} \) and \( x = 5\, \text{cm} \). Calculate: (a) the net outward flux through the cylinder, and (b) the net charge inside the cylinder.- CBSE CLASS XII - 2025
- Physics
- Electric Flux
A line charge of length \( \frac{a}{2} \) is kept at the center of an edge BC of a cube ABCDEFGH having edge length \( a \). If the density of the line is \( \lambda C \) per unit length, then the total electric flux through all the faces of the cube will be : (Take \( \varepsilon_0 \) as the free space permittivity)

- JEE Main - 2025
- Physics
- Electric Flux
A metallic sphere of radius \( R \) carrying a charge \( q \) is kept at a certain distance from another metallic sphere of radius \( R_4 \) carrying a charge \( Q \). What is the electric flux at any point inside the metallic sphere of radius \( R \) due to the sphere of radius \( R_4 \)?

- KCET - 2025
- Physics
- Electric Flux
- The angle between the particle velocity and wave velocity in a transverse wave is (except when the particle passes through the mean position)
- KCET - 2025
- Physics
- Electric Flux
- A charge is kept at the central point P of a cylindrical region. The two edges subtend a half-angle \(\theta\) at P, as shown in the figure. When \(\theta = 30\) , then the electric flux through the curved surface of the cylinder is \(Φ\). If \(\theta= 60\degree\) , then the electric flux through the curved surface becomes \(Φ/√𝑛\), where the value of n is______.
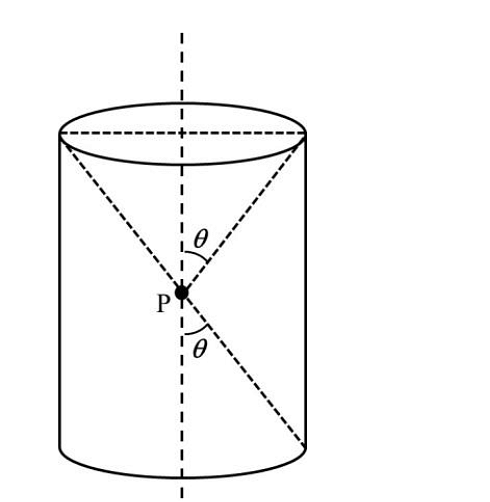
- JEE Advanced - 2024
- Physics
- Electric Flux
Questions Asked in KCET exam
- The mean deviation about the mean for the data \( 4, 7, 8, 9, 10, 12, 13, 17 \) is:
- KCET - 2025
- measurement of angles
- The distance of the point \( P(-3,4,5) \) from the yz-plane is:
- KCET - 2025
- Distance of a Point From a Line
- If 'a' and 'b' are the order and degree respectively of the differentiable equation \[ \frac{d^2 y}{dx^2} + \left(\frac{dy}{dx}\right)^3 + x^4 = 0, \quad \text{then} \, a - b = \, \_ \_ \]
- KCET - 2025
- Differential equations
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- If \( A \) is a square matrix of order \( 3 \times 3 \), \( \det A = 3 \), then the value of \( \det(3A^{-1}) \) is:
- KCET - 2025
- Matrices