The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by
Show Hint
When the magnetic flux linked with a circuit changes, an emf is induced in the circuit that stays as long as the flux keeps changing.
- $Q=\frac{1}{R}.\frac{Δ\phi}{Δt}$
- $Q=\frac{Δ\phi}{R}$
- $Q=\frac{Δ\phi}{Δt}$
- $Q=R.\frac{Δ\phi}{Δt}$
The Correct Option is B
Approach Solution - 1
As, e = \(| {ΔΦ \over Δt} |\)
Current or I = e/R = ΔΦ/RΔt
So, charge Q = IΔt
= ΔΦ/RΔt . Δt
= ΔΦ/R
Therefore, option B is the correct answer.
Approach Solution -2
Using the concept of Faraday’s law of EMI. By using this concept, we can find the total amount of charges passing through the circuit to get the required solution.
Formula used: \(e=\frac{Δϕ}{Δt}\)
Where,
- e is the induced voltage,
- ΔΦ is the change in magnetic flux
- Δt is the change in time.
From Faraday’s law of EMI, the emf induced in the circuit is given as,
\(e=\frac{Δϕ}{Δt}\)
And if R is the resistance in the circuit then -
\(I=\frac{e}{R}\)
\(⇒I=\frac{Δϕ}{Δt.R}\)
The total amount of charge that passes through the circuit becomes -
\(∵Q=I×Δt\)
\(⇒Q=\frac{Δϕ}{Δt.R}.Δt\)
\(⇒Q=\frac{Δϕ}{R}\)
So, the total amount of charge passing through the circuit is given by \(\frac{Δϕ}{R}\).
The magnetic flux through a circuit of resistance R changes by an amount Δϕ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by ΔΦ/R.
Hence, the correct option is B.
Note: When the magnetic flux linked with a circuit changes, an emf is induced in the circuit that stays as long as the flux keeps changing. The induced emf opposes the cause due to which it is produced.
Top Questions on Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )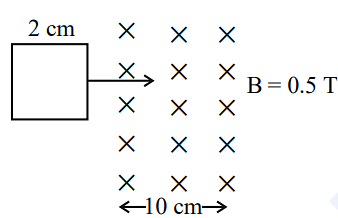
- KCET - 2023
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
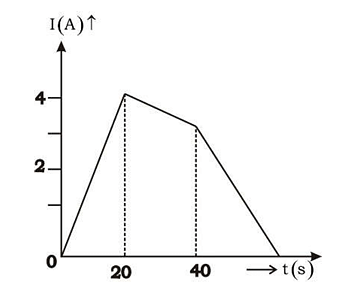
- KCET - 2021
- Physics
- Faradays laws of induction
Questions Asked in NEET exam
- In some appropriate units, time (t) and position (x) relation of a moving particle is given by \(t = \alpha x^2 + \beta x\). The acceleration of the particle is :
- NEET (UG) - 2025
- Kinematic equations for uniformly accelerated motion
The output (Y) of the given logic implementation is similar to the output of an/a …………. gate.

- NEET (UG) - 2025
- Logic gates
- Two identical point masses P and Q, suspended from two separate massless springs of spring constants \(k_1\) and \(k_2\), respectively, oscillate vertically. If their maximum velocities are the same, the ratio of the amplitude of P to the amplitude of Q is :
- NEET (UG) - 2025
- Waves and Oscillations
- A particle of mass \(m\) is moving around the origin with a constant speed \(v\) along a circular path of radius \(R\). When the particle is at \( (0, R) \), its velocity is \( \mathbf{v} = -v \hat{\mathbf{i}} \). The angular momentum of the particle with respect to the origin is :
- NEET (UG) - 2025
- The Angular Momentum
- The radius of Martian orbit around the Sun is about 1.5 times the radius of the orbit of Mercury. The Martian year is 687 Earth days. Then which of the following is the length of 1 year on Mercury?
- NEET (UG) - 2025
- Kepler’s laws
Concepts Used:
Faradays Laws of Induction
There are two laws, given by Faraday which explain the phenomena of electromagnetic induction:
Faraday's First Law:
Whenever a conductor is placed in a varying magnetic field, an emf is induced. If the conductor circuit is closed, a current is induced, known as the induced current.
Faraday's Second Law:
The Emf induced inside a coil is equal to the rate of change of associated magnetic flux.
This law can be mathematically written as:
∈\(-N {\triangle \phi \over \triangle t}\)
