The Integral
\(\int \frac{(1 - \frac{1}{\sqrt{3}})(\cos x - \sin x)}{1 + \frac{2}{\sqrt{3}}\sin2 x} \,dx\)
is equal to
The Integral
\(\int \frac{(1 - \frac{1}{\sqrt{3}})(\cos x - \sin x)}{1 + \frac{2}{\sqrt{3}}\sin2 x} \,dx\)
is equal to
\(\frac{1}{2} \log_e \left| \frac{\tan\left(\frac{\pi}{2} + \frac{\pi}{12}\right)}{\tan\left(\frac{\pi}{2} + \frac{\pi}{6}\right)} \right| + C\)
\(\frac{1}{2} \log_e \left| \frac{\tan\left(\frac{\pi}{2} + \frac{\pi}{6}\right)}{\tan\left(\frac{\pi}{2} + \frac{\pi}{3}\right)} \right| + C\)
\(\log_e \left| \frac{\tan\left(\frac{\pi}{2} + \frac{\pi}{6}\right)}{\tan\left(\frac{\pi}{2} + \frac{\pi}{12}\right)} \right| + C\)
\(\frac{1}{2} \log_e \left| \frac{\tan\left(\frac{\pi}{2} - \frac{\pi}{12}\right)}{\tan\left(\frac{\pi}{2} - \frac{\pi}{6}\right)} \right| + C\)
The Correct Option is A
Solution and Explanation
The correct answer is (A) : \(\frac{1}{2} \log_e \left| \frac{\tan\left(\frac{\pi}{2} + \frac{\pi}{12}\right)}{\tan\left(\frac{\pi}{2} + \frac{\pi}{6}\right)} \right| + C\)
\(=\int \frac{(1 - \frac{1}{\sqrt{3}})(\cos x - \sin x)}{1 + \frac{2}{\sqrt{3}}\sin2 x} \,dx\)
\(= ∫\frac{(\frac{\sqrt{3}-1}{\sqrt{3}}) \sqrt2\sin(\frac{π}{4}-x)}{(\frac{2}{\sqrt3})(\sin \frac{π}{3}+\sin 2x)}dx\)
\(= ∫ \frac{\frac{(\sqrt{3}-1)}{\sqrt2}\sin(\frac{π}{4}-x)}{\sin(\frac{π}{3}+\sin2x)}dx\)
\(=\int \frac{\frac{\sqrt{3}-1}{2\sqrt{2}}\sin(\frac{\pi}{4}-x)}{\sin(\frac{\pi}{6}+x)\cos(\frac{\pi}{6}-x)} \,dx\)
\(= \frac{1}{2} ∫ \frac{2\sin\frac{π}{12}sin(\frac{π}{4}-x) }{\sin(\frac{π}{6}+x)\cos(\frac{π}{6}-x)}dx\)
\(= \frac{1}{2} ∫ \frac{\cos(\frac{π}{6}-x)-\cos(\frac{π}{3}-x)}{\sin(\frac{π}{6}+x)\cos(\frac{π}{6}-x)}dx\)
\(=\frac{1}{2} [ ∫\cosec (\frac{π}{6}+x)dx - ∫sec (\frac{π}{6}-x)dx]\)
\(=\frac{1}{2}[In |\tan(\frac{π}{12}+\frac{x}{2})|- ∫\cosec (\frac{π}{3}-x)dx]\)
\(=\frac{1}{2} [ In|\tan(\frac{π}{12}+ \frac{π}{2})| -In| \frac{π}{6}+\frac{π}{2}|] +C\)
\(=\frac{1}{2} In|\frac{\tan(\frac{π}{12}+ \frac{π}{2})}{\tan(\frac{π}{6}+ \frac{π}{2})}| +C\)
Top Questions on Definite Integral
- Evaluate the definite integral: \( \int_{-2}^{2} |x^2 - x - 2| \, dx \)
- MHT CET - 2025
- Mathematics
- Definite Integral
- For \( x \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \), if\[y(x) = \int \frac{\csc x + \sin x}{\csc x \sec x + \tan x \sin^2 x} \, dx\]and\[\lim_{x \to -\frac{\pi}{2}} y(x) = 0\]then \( y\left(\frac{\pi}{4}\right) \) is equal to
- JEE Main - 2024
- Mathematics
- Definite Integral
- The value of the integral \[ \int_{-1}^{2} \log_e \left( x + \sqrt{x^2 + 1} \right) \, dx \] is:
- JEE Main - 2024
- Mathematics
- Definite Integral
The value \( 9 \int_{0}^{9} \left\lfloor \frac{10x}{x+1} \right\rfloor \, dx \), where \( \left\lfloor t \right\rfloor \) denotes the greatest integer less than or equal to \( t \), is ________.
- JEE Main - 2024
- Mathematics
- Definite Integral
- The value of \(\lim_{{n \to \infty}} \sum_{{k=1}}^{n} \frac{n^3}{{(n^2 + k^2)(n^2 + 3k^2)}}\) is
- JEE Main - 2024
- Mathematics
- Definite Integral
Questions Asked in JEE Main exam
- The moment of inertia of a square loop made of four uniform solid cylinders, each having radius R and length L (\(R \le L\)) about an axis passing through the mid points of opposite sides, is (Take the mass of the entire loop as M) :
- JEE Main - 2026
- Kinematics
Which of the following best represents the temperature versus heat supplied graph for water, in the range of \(-20^\circ\text{C}\) to \(120^\circ\text{C}\)?

- JEE Main - 2026
- Thermodynamics
- When a part of a straight capillary tube is placed vertically in a liquid, the liquid rises upto certain height \( h \). If the inner radius of the capillary tube, density of the liquid and surface tension of the liquid decrease by \(1%\) each, then the height of the liquid in the tube will change by ________ %.
- JEE Main - 2026
- thermal properties of matter
- A gas of certain mass filled in a closed cylinder at a pressure of $3.23\,\text{kPa}$ has temperature $50^\circ$C. The gas is now heated to double its temperature. The modified pressure is ___ Pa.
- JEE Main - 2026
- Thermodynamics
- Let the circle \(x^2+y^2=4\) intersect the \(x\)-axis at points \(A(a,0)\) and \(B(b,0)\). Let \(P(2\cos\alpha,2\sin\alpha)\), \(0<\alpha<\frac{\pi}{2}\), and \(Q(2\cos\beta,2\sin\beta)\) be two points on the circle such that \((\alpha-\beta)=\frac{\pi}{2}\). Then the point of intersection of lines \(AQ\) and \(BP\) lies on:
- JEE Main - 2026
- Circles
Concepts Used:
Definite Integral
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
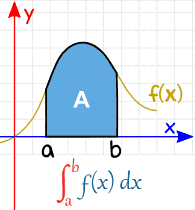
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below: