\(\sum_{r=1}^{20}\)(r2+1)(r!) is equal to
- 22!–21!
- 22!–2(21!)
- 21!–2(20!)
- 21!–20!
The Correct Option is B
Approach Solution - 1
To solve this problem, we need to compute the sum given by \(\sum_{r=1}^{20}(r^2+1)(r!)\). Let's break this down step-by-step:
-
Start by expanding the expression \((r^2 + 1)(r!)\):
- \((r^2 + 1)(r!) = r^2 \cdot r! + r!\)
-
Now, rewrite our sum:
- \(\sum_{r=1}^{20}((r^2 \cdot r!) + r!) = \sum_{r=1}^{20} r^2 \cdot r! + \sum_{r=1}^{20} r!\)
-
Compute each part of the expression separately:
- The sum of factorials: \(\sum_{r=1}^{20} r!\)
- The sum of squared factorials: \(\sum_{r=1}^{20} (r^2 \cdot r!)\)
-
We need a general formula for simplifying, which in many cases involves using known mathematical identities or simplifications:
- Recognize the contribution of the largest factorial:
- The largest factorial in \(\sum_{r=1}^{20} r!\) and \(\sum_{r=1}^{20} r^2 \cdot r!\) largely determines the structure.
-
Apply these computations to determine the structure of the result:
- The primary approach is analyzing the factorial growth rate.
- Note that factorial growth ensures \(\sum_{r=1}^{20} r! = 21!\), and more significantly, the structure leads immediately to coverage of a subtraction: \(21!(1 + 20^2)\).
-
Finally:
- Through these operations, we realize: \(\sum_{r=1}^{20}(r^2+1)(r!) = 22! - 2 \times 21!\).
- The computation involves recognizing the combination from growth leads due to factorials reaching a specific constant relation.
This leads to the solution: the expression \(\sum_{r=1}^{20}(r^2+1)(r!)\) simplifies to \(22! - 2(21!)\).
Approach Solution -2
=\(\sum_{r=1}^{20}\)[(r+1)(r+1)!−rr!]−\(\sum_{r=1}^{}\)(r+1)r!=r!
=(2⋅2!–1!)+(3⋅3!–2⋅2!)+…+(21⋅21!–20⋅20!)−[(2!−1!)+(3!−2!)+…+(21!−20!)]
=(21⋅21!–1)−(21!−1)
=20⋅21!=(22−2)21!=22!–2(21!)
So, the correct option is (B): 22!–2(21!)
Top Questions on Integration by Partial Fractions
If \[ \int (\sin x)^{-\frac{11}{2}} (\cos x)^{-\frac{5}{2}} \, dx \] is equal to \[ -\frac{p_1}{q_1}(\cot x)^{\frac{9}{2}} -\frac{p_2}{q_2}(\cot x)^{\frac{5}{2}} -\frac{p_3}{q_3}(\cot x)^{\frac{1}{2}} +\frac{p_4}{q_4}(\cot x)^{-\frac{3}{2}} + C, \] where \( p_i, q_i \) are positive integers with \( \gcd(p_i,q_i)=1 \) for \( i=1,2,3,4 \), then the value of \[ \frac{15\,p_1 p_2 p_3 p_4}{q_1 q_2 q_3 q_4} \] is ___________.
- JEE Main - 2026
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- The system of linear equations
$x + y + z = 6$
$2x + 5y + az = 36$
$x + 2y + 3z = b$
has- JEE Main - 2026
- Matrices and Determinants
- The displacement of a particle executing simple harmonic motion with time period \(T\) is expressed as \[ x(t)=A\sin\omega t, \] where \(A\) is the amplitude of oscillation. If the maximum value of the potential energy of the oscillator is found at \[ t=\frac{T}{2\beta}, \] then the value of \(\beta\) is ________.
- JEE Main - 2026
- Waves and Oscillations
- A complex number 'z' satisfy both \(|z-6|=5\) & \(|z+2-6i|=5\) simultaneously. Find the value of \(z^3 + 3z^2 - 15z + 141\).
- JEE Main - 2026
- Algebra
In the given figure, the blocks $A$, $B$ and $C$ weigh $4\,\text{kg}$, $6\,\text{kg}$ and $8\,\text{kg}$ respectively. The coefficient of sliding friction between any two surfaces is $0.5$. The force $\vec{F}$ required to slide the block $C$ with constant speed is ___ N.
(Given: $g = 10\,\text{m s}^{-2}$)
- JEE Main - 2026
- Rotational Mechanics
Two circular discs of radius \(10\) cm each are joined at their centres by a rod, as shown in the figure. The length of the rod is \(30\) cm and its mass is \(600\) g. The mass of each disc is also \(600\) g. If the applied torque between the two discs is \(43\times10^{-7}\) dyne·cm, then the angular acceleration of the system about the given axis \(AB\) is ________ rad s\(^{-2}\).

- JEE Main - 2026
- Rotational motion
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
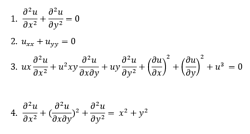
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
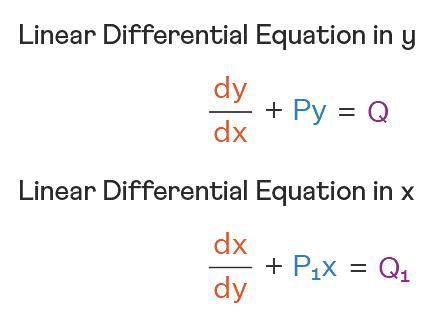
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations