Let \(P1:\overrightarrow{r}.(2\^i+\^j−3\^k )=4\) be a plane. Let \(P_2\) be another plane which passes through points \((2, - 3, 2)\), \((2, - 2, -3)\) and \((1, -4, 2)\). If the direction ratios of the line of intersection of \(P_1\) and \(P_2\) be \(16, α,β,\) then the value of \(α + β\) is equal to _____ .
Correct Answer: 28
Solution and Explanation
Direction ratio of normal to \(P_1≡< 2, 1, – 3 >\)
and \(P2≡\begin{vmatrix} \hat i & \hat j & \hat k \\[0.3em] 0 & 1 & -5 \\[0.3em] -1 & -2 & 5 \end{vmatrix}\)
\(P_2=−5\hat i−\hat j(−5)+\hat k(1)\)
i.e.\(< –5, 5, 1 >\)
d.r’s of line of intersection are along vector
\(\begin{vmatrix} \hat i & \hat j & \hat k \\[0.3em] 2 & 1 & -3 \\[0.3em] -5 & 5 & 1 \end{vmatrix}\)\(=\hat i(16)−\hat j(−13)+\hat k(15)\)
i.e.\(< 16, 13, 15 >\)
Therefore, \(α + β = 13 + 15 = 28\)
So, the answer is \(28\).
Top Questions on Plane
- Let the foot of perpendicular from a point \( P(1,2,-1) \) to the straight line \( L : \frac{x}{1} = \frac{y}{0} = \frac{z}{-1} \) be \( N \). Let a line be drawn from \( P \) parallel to the plane \( x + y + 2z = 0 \) which meets \( L \) at point \( Q \). If \( \alpha \) is the acute angle between the lines \( PN \) and \( PQ \), then \( \cos \alpha \) is equal to:
- Let R be the relation "is congruent to" on the set of all triangles in a plane. Is R:
- Let the acute angle bisector of the two planes \( x - 2y - 2z + 1 = 0 \) and \( 2x - 3y - 6z + 1 = 0 \) be the plane \( P \). Then which of the following points lies on \( P \)?
- If the plane \[ x - y + z + 4 = 0 \] divides the line joining the points \[ P(2,3,-1) \quad {and} \quad Q(1,4,-2) \] in the ratio \( l:m \), then \( l + m \) is:
- The equation of the plane passing through the point \( (1, 1, 1) \) and perpendicular to the planes \( 2x + y - 2z = 5 \) and \( 3x - 6y - 2z = 7 \) is:
Questions Asked in JEE Main exam
Let one focus of the hyperbola \( H : \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1 \) be at \( (\sqrt{10}, 0) \) and the corresponding directrix be \( x = \dfrac{9}{\sqrt{10}} \). If \( e \) and \( l \) respectively are the eccentricity and the length of the latus rectum of \( H \), then \( 9 \left(e^2 + l \right) \) is equal to:
- JEE Main - 2025
- Conic sections
- Let \( \alpha_1 \) and \( \beta_1 \) be the distinct roots of \( 2x^2 + (\cos\theta)x - 1 = 0, \ \theta \in (0, 2\pi) \). If \( m \) and \( M \) are the minimum and the maximum values of \( \alpha_1 + \beta_1 \), then \( 16(M + m) \) equals:
- JEE Main - 2025
- Maxima and Minima
- Let the line \( x + y = 1 \) meet the circle \( x^2 + y^2 = 4 \) at the points A and B. If the line perpendicular to AB and passing through the midpoint of the chord AB intersects the circle at C and D, then the area of the quadrilateral ABCD is equal to:
- JEE Main - 2025
- Coordinate Geometry
- The number of different 5 digit numbers greater than 50000 that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, 7, such that the sum of their first and last digits should not be more than 8, is:
- JEE Main - 2025
- permutations and combinations
- Two identical symmetric double convex lenses of focal length \( f \) are cut into two equal parts \( L_1, L_2 \) by the AB plane and \( L_3, L_4 \) by the XY plane as shown in the figure respectively. The ratio of focal lengths of lenses \( L_1 \) and \( L_3 \) is:

Concepts Used:
Distance of a Point from a Plane
The shortest perpendicular distance from the point to the given plane is the distance between point and plane. In simple terms, the shortest distance from a point to a plane is the length of the perpendicular parallel to the normal vector dropped from the particular point to the particular plane. Let's see the formula for the distance between point and plane.
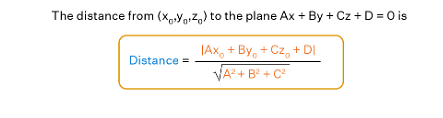
Read More: Distance Between Two Points