Let . If , then is:
The Correct Option is A
Solution and Explanation
Given:We have to find the value of if Consider:After comparing, we get....(i)....(ii)Adding equation (i) and (ii)Hence, the correct option is (A).
Top Questions on Transpose of a Matrix
If the matrix $ A $ is such that $ A \begin{pmatrix} -1 & 2 \\ 3 & 1 \end{pmatrix} = \begin{pmatrix} -4 & 1 \\ 7 & 7 \end{pmatrix} \text{ then } A \text{ is equal to} $
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
If $A = \begin{bmatrix} 5a & -b \\ 3 & 2 \end{bmatrix} \quad \text{and} \quad A \, \text{adj} \, A = A A^t, \quad \text{then} \, 5a + b \, \text{is equal to}$
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
If $3A + 4B^{t} = \left( \begin{array}{cc} 7 & -10 \\ 0 & 6 \end{array} \right) $ and $ 2B - 3A^{t} = \left( \begin{array}{cc} -1 & 18 \\ 4 & -6 \\ -5 & -7 \end{array} \right) $, then find $ (5B)^{t}$:
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
- If \( A = \begin{bmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix} \), then \( A^{-1} \) is:
- MHT CET - 2024
- Mathematics
- Transpose of a Matrix
- If \[ B = \begin{bmatrix} 3 & \alpha & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix} \] is the adjoint of a 3x3 matrix \( A \) and \( |A| = 4 \), then \( \alpha \) is equal to:
- MHT CET - 2024
- Mathematics
- Transpose of a Matrix
Questions Asked in JEE Main exam
- Given below are two statements about X-ray spectra of elements:
Statement (I):A plot of \(\sqrt {v}\) (v=frequency of X-rays emitted) vs atomic mass is a straight line.
Statement (II): A plot of v (v=frequency of X-rays emitted)} vs atomic number is a straight line.- JEE Main - 2025
- X-ray Spectra and Moseley's Law
For the thermal decomposition of \( N_2O_5(g) \) at constant volume, the following table can be formed, for the reaction mentioned below: \[ 2 N_2O_5(g) \rightarrow 2 N_2O_4(g) + O_2(g) \] Given: Rate constant for the reaction is \( 4.606 \times 10^{-2} \text{ s}^{-1} \).
- JEE Main - 2025
- Organic Chemistry
- The ratio of the power of a light source \( S_1 \) to that of the light source \( S_2 \) is 2. \( S_1 \) is emitting \( 2 \times 10^{15} \) photons per second at 600 nm. If the wavelength of the source \( S_2 \) is 300 nm, then the number of photons per second emitted by \( S_2 \) is \_\_\_\_\_ \( \times 10^{14} \).
- JEE Main - 2025
- Units and measurement
- In a group of 3 girls and 4 boys, there are two boys \( B_1 \) and \( B_2 \). The number of ways in which these girls and boys can stand in a queue such that all the girls stand together, all the boys stand together, but \( B_1 \) and \( B_2 \) are not adjacent to each other, is:
- JEE Main - 2025
- Permutations
Let \( T_r \) be the \( r^{\text{th}} \) term of an A.P. If for some \( m \), \( T_m = \dfrac{1}{25} \), \( T_{25} = \dfrac{1}{20} \), and \( \displaystyle\sum_{r=1}^{25} T_r = 13 \), then \( 5m \displaystyle\sum_{r=m}^{2m} T_r \) is equal to:
- JEE Main - 2025
- Arithmetic and Geometric Progressions
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:
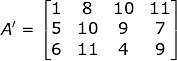
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix