Comprehension
In the circuit shown below, the switch $S$ is connected to position $P$ for a long time so that the charge on the capacitor becomes $q _{1}\, \mu C$. Then $S$ is switched to position $Q$. After a long time, the charge on the capacitor is $q _{2}\, \mu C$
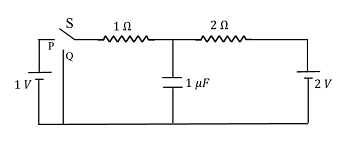

Question: 1
The magnitude of q1 is _____.
The magnitude of q1 is _____.
Updated On: May 9, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 1.33
Solution and Explanation
Step 1: Understanding the given data
We are given the following information:
- Switch \( S \) is at position \( P \), and after a long time, the potential difference across the capacitor branch is:
\[ \frac{4 \times 1}{3} = \frac{4}{3} \, \text{V} \] - The charge on the capacitor is denoted as \( q_1 \) in microcoulombs (\( \mu C \)).
Step 2: Applying the formula for charge on the capacitor
The charge \( q_1 \) on a capacitor is related to the potential difference across the capacitor and its capacitance \( C \) by the equation:
\[ q = C \times V \] where \( V \) is the potential difference and \( C \) is the capacitance.
In this case, the potential difference is given as \( \frac{4}{3} \) V, and from the information provided, we can deduce that the charge on the capacitor \( q_1 \) is also \( \frac{4}{3} \) microcoulombs, as it is related to the potential difference.
Step 3: Conclusion
Therefore, the charge on the capacitor is:
\[ q_1 = \frac{4}{3} \, \mu C = 1.33 \, \mu C \]
We are given the following information:
- Switch \( S \) is at position \( P \), and after a long time, the potential difference across the capacitor branch is:
\[ \frac{4 \times 1}{3} = \frac{4}{3} \, \text{V} \] - The charge on the capacitor is denoted as \( q_1 \) in microcoulombs (\( \mu C \)).
Step 2: Applying the formula for charge on the capacitor
The charge \( q_1 \) on a capacitor is related to the potential difference across the capacitor and its capacitance \( C \) by the equation:
\[ q = C \times V \] where \( V \) is the potential difference and \( C \) is the capacitance.
In this case, the potential difference is given as \( \frac{4}{3} \) V, and from the information provided, we can deduce that the charge on the capacitor \( q_1 \) is also \( \frac{4}{3} \) microcoulombs, as it is related to the potential difference.
Step 3: Conclusion
Therefore, the charge on the capacitor is:
\[ q_1 = \frac{4}{3} \, \mu C = 1.33 \, \mu C \]
Was this answer helpful?
0
0
Question: 2
The magnitude of q2 is_____.
The magnitude of q2 is_____.
Updated On: May 9, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 0.67
Solution and Explanation
Step 1: Understanding the given data
We are given the following information:
- Switch \( S \) is at position \( Q \), and after a long time, the potential difference across the capacitor is equal to the potential difference across a resistance of \( 1 \, \Omega \).
- The charge on the capacitor is denoted as \( q_2 \) in microcoulombs (\( \mu C \)), and it is given as \( \frac{2}{3} \, \mu C \).
Step 2: Relation between potential difference and charge on capacitor
The charge on the capacitor \( q_2 \) is related to the potential difference \( V \) across the capacitor and its capacitance \( C \) by the equation:
\[ q_2 = C \times V \] where \( C \) is the capacitance and \( V \) is the potential difference.
Since the potential difference across the capacitor is equal to the potential difference across the resistance of \( 1 \, \Omega \), we can use the given charge formula to find the charge.
Step 3: Conclusion
The given charge on the capacitor is \( q_2 = \frac{2}{3} \, \mu C \), which simplifies to:
\[ q_2 = 0.67 \, \mu C \]
We are given the following information:
- Switch \( S \) is at position \( Q \), and after a long time, the potential difference across the capacitor is equal to the potential difference across a resistance of \( 1 \, \Omega \).
- The charge on the capacitor is denoted as \( q_2 \) in microcoulombs (\( \mu C \)), and it is given as \( \frac{2}{3} \, \mu C \).
Step 2: Relation between potential difference and charge on capacitor
The charge on the capacitor \( q_2 \) is related to the potential difference \( V \) across the capacitor and its capacitance \( C \) by the equation:
\[ q_2 = C \times V \] where \( C \) is the capacitance and \( V \) is the potential difference.
Since the potential difference across the capacitor is equal to the potential difference across the resistance of \( 1 \, \Omega \), we can use the given charge formula to find the charge.
Step 3: Conclusion
The given charge on the capacitor is \( q_2 = \frac{2}{3} \, \mu C \), which simplifies to:
\[ q_2 = 0.67 \, \mu C \]
Was this answer helpful?
0
0
Top Questions on Capacitors and Capacitance
- A parallel plate capacitor consisting of two circular plates of radius 10 cm is being charged by a constant current of 0.15 A. If the rate of change of potential difference between the plates is \( 7 \times 10^6 \, \text{V/s} \), then the integer value of the distance between the parallel plates is:
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
- A capacitor, \( C_1 = 6 \, \mu F \), is charged to a potential difference of \( V_1 = 5 \, \text{V} \) using a 5V battery. The battery is removed and another capacitor, \( C_2 = 12 \, \mu F \), is inserted in place of the battery. When the switch 'S' is closed, the charge flows between the capacitors for some time until equilibrium condition is reached. What are the charges \( q_1 \) and \( q_2 \) on the capacitors \( C_1 \) and \( C_2 \) when equilibrium condition is reached?

- JEE Main - 2025
- Physics
- Capacitors and Capacitance
- The position of a particle moving on x-axis is given by \( x(t) = A \sin t + B \cos^2 t + Ct^2 + D \), where \( t \) is time. The dimension of \( \frac{ABC}{D} \) is:
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
Identify the valid statements relevant to the given circuit at the instant when the key is closed.

\( \text{A} \): There will be no current through resistor R.
\( \text{B} \): There will be maximum current in the connecting wires.
\( \text{C} \): Potential difference between the capacitor plates A and B is minimum.
\( \text{D} \): Charge on the capacitor plates is minimum.
Choose the correct answer from the options given below:- JEE Main - 2025
- Physics
- Capacitors and Capacitance
- A parallel-plate capacitor of capacitance 40µF is connected to a 100 V power supply. Now the intermediate space between the plates is filled with a dielectric material of dielectric constant K = 2. Due to the introduction of dielectric material, the extra charge and the change in the electrostatic energy in the capacitor, respectively, are -
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
View More Questions
Questions Asked in JEE Advanced exam
Let $ y(x) $ be the solution of the differential equation $$ x^2 \frac{dy}{dx} + xy = x^2 + y^2, \quad x > \frac{1}{e}, $$ satisfying $ y(1) = 0 $. Then the value of $ 2 \cdot \frac{(y(e))^2}{y(e^2)} $ is ________.
- JEE Advanced - 2025
- Differential equations
- The correct order of the wavelength maxima of the absorption band in the ultraviolet-visible region for the given complexes is:
- JEE Advanced - 2025
- coordination compounds
- Calculate the sum of magnetic moments (in Bohr Magnetons, B.M.) of the complexes: \[ [\mathrm{MnCl}_6]^{3-} \quad \text{and} \quad [\mathrm{Mn(CN)}_6]^{3-} \]
- JEE Advanced - 2025
- coordination compounds
- Consider the depicted hydrogen (H) in the hydrocarbons given below. The most acidic hydrogen (H) is:
- JEE Advanced - 2025
- Acids and Bases
- Consider a star of mass $ m_2 $ kg revolving in a circular orbit around another star of mass $ m_1 $ kg with $ m_1 \gg m_2 $. The heavier star slowly acquires mass from the lighter star at a constant rate of $ \gamma $ kg/s. In this transfer process, there is no other loss of mass. If the separation between the centers of the stars is $ r $, then its relative rate of change $ \frac{1}{r} \frac{dr}{dt} $ (in s$^{-1}$) is given by:
- JEE Advanced - 2025
- Gravitation
View More Questions