Question:
In a series LCR circuit connected to an AC source, at resonance, the current is maximum because:
In a series LCR circuit connected to an AC source, at resonance, the current is maximum because:
Show Hint
At resonance in a series LCR circuit, inductive and capacitive reactances cancel, minimizing impedance and maximizing current.
Updated On: Jan 13, 2026
- The inductive reactance is maximum
- The capacitive reactance cancels the inductive reactance
- The resistance is zero
- The reactances add up
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
In a series LCR circuit, the total impedance (\( Z \)) is given by:
\[ Z = \sqrt{R^2 + (X_L - X_C)^2} \]
where:
- \( R \) is the resistance
- \( X_L = \omega L \) is the inductive reactance
- \( X_C = \frac{1}{\omega C} \) is the capacitive reactance
At resonance, \( X_L = X_C \), so:
\[ Z = \sqrt{R^2 + (X_L - X_C)^2} = \sqrt{R^2} = R \]
The impedance is minimized, leading to maximum current as per Ohm's law:
\[ I = \frac{V}{Z} \]
Hence, the current is maximum because inductive and capacitive reactances cancel each other.
Was this answer helpful?
0
0
Top Questions on Amperes circuital law
Consider the circuit shown :
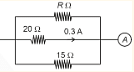 The ammeter reads 0.9 A. Value of R is
The ammeter reads 0.9 A. Value of R is- JEE Main - 2024
- Physics
- Amperes circuital law
- A coil has a resistance of \( 30 \, \Omega \) and an inductive reactance of \( 20 \, \Omega \) at 50 Hz frequency. If an AC source of 200 V and 100 Hz is connected across the coil, then how much current will flow through the coil?
- MHT CET - 2024
- Physics
- Amperes circuital law
- Among the following, Ampere’s circuital law is represented by:
- AP EAPCET - 2023
- Physics
- Amperes circuital law
- In the given circuit, find the voltage drop VL in the load resistance RL

- WBJEE - 2023
- Physics
- Amperes circuital law
- A transistor is used in an amplifier circuit in common emitter mode. If the base current changes by 100μA, it brings a change of 10mA in collector current. If the load resistance is 2kΩ and input resistance is 1kΩ, the value of power gain is \(x×10^4\). The value of x is _______.
- JEE Main - 2022
- Physics
- Amperes circuital law
View More Questions
Questions Asked in MHT CET exam
- What is the volume occupied by 2 moles of an ideal gas at standard temperature and pressure (STP)?
- MHT CET - 2025
- States of matter
- Evaluate the integral: \[ \int \frac{\sqrt{\tan x}}{\sin x \cos x} \, dx \]
- MHT CET - 2025
- Integration
- Let \( \mathbf{a} \), \( \mathbf{b} \), and \( \mathbf{c} \) be vectors of magnitude 2, 3, and 4 respectively. If: - \( \mathbf{a} \) is perpendicular to \( (\mathbf{b} + \mathbf{c}) \), - \( \mathbf{b} \) is perpendicular to \( (\mathbf{c} + \mathbf{a}) \), - \( \mathbf{c} \) is perpendicular to \( (\mathbf{a} + \mathbf{b}) \), then the magnitude of \( \mathbf{a} + \mathbf{b} + \mathbf{c} \) is equal to:
- MHT CET - 2025
- Vectors
- A die was thrown \( n \) times until the lowest number on the die appeared. If the mean is \( \frac{n}{g} \), then what is the value of \( n \)?
- MHT CET - 2025
- Probability
- Which of the following has the lowest boiling point?
- MHT CET - 2025
- intermolecular forces
View More Questions