In the given circuit, find the voltage drop VL in the load resistance RL
- 5V
- 3V
- 9V
- 6V
The Correct Option is B
Solution and Explanation
The voltage drop across the load resistance (VL) in a circuit can be determined using Ohm's Law (V=I⋅R), where V is voltage, I is current, and R is resistance. Since the load resistance is connected in series with the given 1Ω resistor and the 2V voltage source, the total resistance in the circuit is total=1Ω+RL.
The total current flowing through the circuit is given by total V source=1Ω+RL2V.
Applying Ohm's Law to the load resistance (VL=I⋅RL), we can substitute the expression for I to find:
VL=1Ω+RL2V⋅RL.
Given that RL is unknown, the given answer of VL=3V might not be correct, as it depends on the specific value of RL. The answer could be correct if RL happens to be 3Ω, resulting in VL=1Ω+3Ω2V⋅3Ω=3V.
The correct option is(B): 3V
Top Questions on Amperes circuital law
Consider the circuit shown :
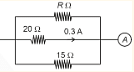The ammeter reads 0.9 A. Value of R is- JEE Main - 2024
- Physics
- Amperes circuital law
- A transistor is used in an amplifier circuit in common emitter mode. If the base current changes by 100μA, it brings a change of 10mA in collector current. If the load resistance is 2kΩ and input resistance is 1kΩ, the value of power gain is \(x×10^4\). The value of x is _______.
- JEE Main - 2022
- Physics
- Amperes circuital law
- A long straight wire with a circular cross-section having radius R, is carrying a steady current I. The current I is uniformly distributed across this cross-section. Then the variation of magnetic field due to current I with distance r (r < R) from its centre
- JEE Main - 2022
- Physics
- Amperes circuital law
- A thick current carrying cable of radius $'R'$ carries current $'I'$ uniformly distributed across its cross-section. The variation of magnetic field $B ( r )$ due to the cable with the distance $'r'$ from the axis of the cable is represented by :
- NEET (UG) - 2021
- Physics
- Amperes circuital law
- Which o f the following is true with respect to Rogers spiral experiment?
- JKCET - 2019
- Physics
- Amperes circuital law
Questions Asked in WBJEE exam
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
- ABC is an isosceles triangle with an inscribed circle with center O. Let P be the midpoint of BC. If AB=AC=15 and BC=10,then OP equals
- WBJEE - 2023
- Three Dimensional Geometry
- Let A=\(\begin{pmatrix} 0&0 &1 \\ 1&0 &0 \\ 0&0 &0 \end{pmatrix}\), B=\(\begin{pmatrix} 0&1 &0 \\ 0&0 &1 \\ 0&0 &0 \end{pmatrix}\) and P=\(\begin{pmatrix} 0&1 &0 \\ x&0 &0 \\ 0&0 &y \end{pmatrix}\) be an orthogonal matrix such that B=PAP-1 holds. Then
- WBJEE - 2023
- Matrices
Let α,β be the roots of the equation, ax2+bx+c=0.a,b,c are real and sn=αn+βn and \(\begin{vmatrix}3 &1+s_1 &1+s_2\\1+s_1&1+s_2 &1+s_3\\1+s_2&1+s_3 &1+s_4\end{vmatrix}=\frac{k(a+b+c)^2}{a^4}\) then k=
- WBJEE - 2023
- Complex Numbers and Quadratic Equations
- An electric dipole of dipole moment p is placed at the origin of the coordinate system along the z-axis. The amount of work required to move a charge 'q' from the point (a,0,0) to the point (0,0,a) is
- WBJEE - 2023
- Electric Dipole
Concepts Used:
LCR Circuit
An LCR circuit, also known as a resonant circuit, or an RLC circuit, is an electrical circuit consist of an inductor (L), capacitor (C) and resistor (R) connected in series or parallel.
Series LCR circuit
When a constant voltage source is connected across a resistor a current is induced in it. This current has a unique direction and flows from the negative to positive terminal. Magnitude of current remains constant.
Alternating current is the current if the direction of current through this resistor changes periodically. An AC generator or AC dynamo can be used as AC voltage source.
