A transistor is used in an amplifier circuit in common emitter mode. If the base current changes by 100μA, it brings a change of 10mA in collector current. If the load resistance is 2kΩ and input resistance is 1kΩ, the value of power gain is \(x×10^4\). The value of x is _______.
Correct Answer: 2
Solution and Explanation
The correct answer is: 2
Power gain
\(=[\frac{\triangle{ic}}{\triangle{iB}}]×\frac{R_0}{R_i}\)
\(=[\frac{10^{-2}}{10^{-4}}]×\frac{2}{1}\)
= 2 × 104
\(⇒ x = 2\)
Top Questions on Amperes circuital law
Consider the circuit shown :
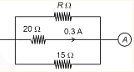The ammeter reads 0.9 A. Value of R is- JEE Main - 2024
- Physics
- Amperes circuital law
- In a series LCR circuit connected to an AC source, at resonance, the current is maximum because:
- MHT CET - 2024
- Physics
- Amperes circuital law
- A coil has a resistance of \( 30 \, \Omega \) and an inductive reactance of \( 20 \, \Omega \) at 50 Hz frequency. If an AC source of 200 V and 100 Hz is connected across the coil, then how much current will flow through the coil?
- MHT CET - 2024
- Physics
- Amperes circuital law
- Among the following, Ampere’s circuital law is represented by:
- AP EAPCET - 2023
- Physics
- Amperes circuital law
- In the given circuit, find the voltage drop VL in the load resistance RL
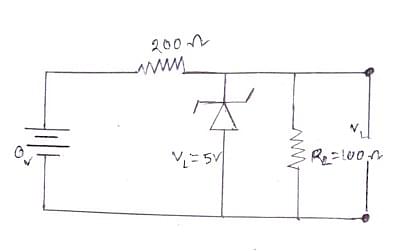
- WBJEE - 2023
- Physics
- Amperes circuital law
Questions Asked in JEE Main exam
Two light beams fall on a transparent material block at point 1 and 2 with angle \( \theta_1 \) and \( \theta_2 \), respectively, as shown in the figure. After refraction, the beams intersect at point 3 which is exactly on the interface at the other end of the block. Given: the distance between 1 and 2, \( d = 4/3 \) cm and \( \theta_1 = \theta_2 = \cos^{-1} \frac{n_2}{2n_1} \), where \( n_2 \) is the refractive index of the block and \( n_1 \) is the refractive index of the outside medium, then the thickness of the block is cm.
- JEE Main - 2025
- Refraction of Light
A bob of mass \(m\) is suspended at a point \(O\) by a light string of length \(l\) and left to perform vertical motion (circular) as shown in the figure. Initially, by applying horizontal velocity \(v_0\) at the point ‘A’, the string becomes slack when the bob reaches at the point ‘D’. The ratio of the kinetic energy of the bob at the points B and C is:
- JEE Main - 2025
- Kinetic Energy
- A vessel at 1000 K contains \( \text{CO}_2 \) with a pressure of 0.5 atm. Some of \( \text{CO}_2 \) is converted into \( \text{CO} \) on addition of graphite. If total pressure at equilibrium is 0.8 atm, then \( K_p \) is:
- JEE Main - 2025
- Equilibrium
Two light beams fall on a transparent material block at point 1 and 2 with angle \( \theta_1 \) and \( \theta_2 \), respectively, as shown in the figure. After refraction, the beams intersect at point 3 which is exactly on the interface at the other end of the block. Given: the distance between 1 and 2, \( d = \frac{4}{3} \) cm and \( \theta_1 = \theta_2 = \cos^{-1} \left( \frac{n_2}{2n_1} \right) \), where \( n_2 \) is the refractive index of the block and \( n_1 \) is the refractive index of the outside medium, then the thickness of the block is …….. cm.
- JEE Main - 2025
- Units and measurement
Let \( y^2 = 12x \) be the parabola and \( S \) its focus. Let \( PQ \) be a focal chord of the parabola such that \( (SP)(SQ) = \frac{147}{4} \). Let \( C \) be the circle described by taking \( PQ \) as a diameter. If the equation of the circle \( C \) is: \[ 64x^2 + 64y^2 - \alpha x - 64\sqrt{3}y = \beta, \] then \( \beta - \alpha \) is equal to:
- JEE Main - 2025
- Parabola
Concepts Used:
Amperes circuital law
According to Ampere’s law, magnetic fields are related to the electric current that is produced in them. This law specifies that the magnetic field is associated with a given current or vice-versa, provided that the electric field doesn’t change with time.
Ampere’s circuital law can be written as the line integral of the magnetic field surrounding the closed loop which is equal to the number of times the algebraic sum of currents passing through the loop.
According to the second equation, if the magnetic field is integrated along the blue path, then it is equal to the current enclosed, I.
The magnetic field doesn’t vary at a distance r because of symmetry. The path length (in blue) in figure 1 has to be equal to the circumference of a circle,2πr.
