Question:
In a magnetic field of $0.05\, T,$ area of a coil changes from $101\, cm^2$ to $100\, cm^2$ without changing the resistance which is $2\,\Omega$. The amount of charge that flow during this period is
In a magnetic field of $0.05\, T,$ area of a coil changes from $101\, cm^2$ to $100\, cm^2$ without changing the resistance which is $2\,\Omega$. The amount of charge that flow during this period is
Updated On: Apr 15, 2024
- $2.5 � 10^{-6}\, C$
- $2 � 10^{-6}\, C$
- $10^{-6}\,C$
- $8 � 10^{-6}\, C$
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Magnetic Flux, $\phi=B\cdot A$
Change in flux, $d\,\phi=B\cdot dA$
$=0.05\left(101-100\right)\times10^{-4}$
$=5\times10^{-6}\,Wb$
Charge $dQ=\frac{d\phi}{R}$
$=\frac{5\times10^{-6}}{2}=2.5\times10^{-6}\,C$
Change in flux, $d\,\phi=B\cdot dA$
$=0.05\left(101-100\right)\times10^{-4}$
$=5\times10^{-6}\,Wb$
Charge $dQ=\frac{d\phi}{R}$
$=\frac{5\times10^{-6}}{2}=2.5\times10^{-6}\,C$
Was this answer helpful?
0
0
Top Questions on Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )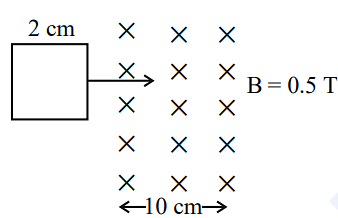
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
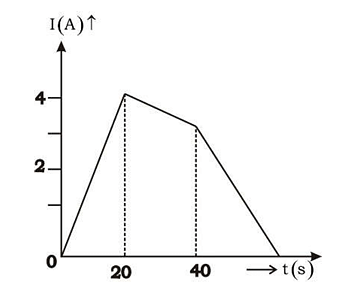
- KCET - 2021
- Physics
- Faradays laws of induction
View More Questions
Questions Asked in VITEEE exam
- Two identical blocks A and B, each of mass 'm' resting on a smooth floor are connected by a light spring of natural length L and spring constant K, with the spring at its natural length. A third identical block 'C' (mass m) moving with a speed v along the line joining A and B collides with A. the maximum compression in the spring is
- VITEEE - 2023
- work, energy and power
- Assertion :
The binding energy of the nucleus increases with the increase in atomic number.
Reason :
Heavier elements have a greater number of non-radioactive isotopes than radioactive isotopes. - The half-life of radioactive radon is 3.8 days. The time at the end of which \(\frac{1}{20}th\) of the Radon sample will remain undecayed is (given log10e=0.4343)
- Which element has more electron gain enthalpy among chalcogen group?
- VITEEE - 2022
- sulphur
- Coin is tossed till heads is obtained what is expectation of no. of coin tosses
- VITEEE - 2022
- Random Variables
View More Questions
Concepts Used:
Faradays Laws of Induction
There are two laws, given by Faraday which explain the phenomena of electromagnetic induction:
Faraday's First Law:
Whenever a conductor is placed in a varying magnetic field, an emf is induced. If the conductor circuit is closed, a current is induced, known as the induced current.
Faraday's Second Law:
The Emf induced inside a coil is equal to the rate of change of associated magnetic flux.
This law can be mathematically written as:
∈\(-N {\triangle \phi \over \triangle t}\)
