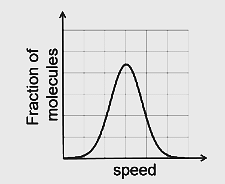
If the distribution of molecular speeds of a gas is as per the figure shown below, then the ratio of the most probable, the average, and the root mean square speeds, respectively, is

- $1: 1: 1$
- $1: 1: 1.224$
- $1: 1.128: 1.224$
- $1: 1.128: 1$
The Correct Option is B
Solution and Explanation
In a symmetrical graph, the average value of speed corresponds to the midpoint, which is also the most probable speed.
However, when calculating the root mean square (rms) speed, we compute the average of the squares of the speeds and then take the square root. Since higher speeds contribute more to the squared value, the result will be higher than the average speed value.
So the Correct Option is (B): $1: 1: 1.224$
Top Questions on kinetics equations
- Magnetic Moment of \( \text{Mn}^{2+} \) is:
- MHT CET - 2024
- Chemistry
- kinetics equations
Find the time required to complete a reaction 90% if the reaction is completed 50% in 15 minutes.
- MHT CET - 2024
- Chemistry
- kinetics equations
- IUPAC Name of Glyceraldehyde is:
- MHT CET - 2024
- Chemistry
- kinetics equations
- IUPAC Name of Acetone is:
- MHT CET - 2024
- Chemistry
- kinetics equations
- The half-life period of a first order reaction is 1000 seconds. Its rate constant is:
- KEAM - 2024
- Chemistry
- kinetics equations
Questions Asked in JEE Advanced exam
- Let $ x_0 $ be the real number such that $ e^{x_0} + x_0 = 0 $. For a given real number $ \alpha $, define $$ g(x) = \frac{3xe^x + 3x - \alpha e^x - \alpha x}{3(e^x + 1)} $$ for all real numbers $ x $. Then which one of the following statements is TRUE?
- JEE Advanced - 2025
- Fundamental Theorem of Calculus
- A linear octasaccharide (molar mass = 1024 g mol$^{-1}$) on complete hydrolysis produces three monosaccharides: ribose, 2-deoxyribose and glucose. The amount of 2-deoxyribose formed is 58.26 % (w/w) of the total amount of the monosaccharides produced in the hydrolyzed products. The number of ribose unit(s) present in one molecule of octasaccharide is _____.
Use: Molar mass (in g mol$^{-1}$): ribose = 150, 2-deoxyribose = 134, glucose = 180; Atomic mass (in amu): H = 1, O = 16- JEE Advanced - 2025
- Biomolecules
Let $ P(x_1, y_1) $ and $ Q(x_2, y_2) $ be two distinct points on the ellipse $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$ such that $ y_1 > 0 $, and $ y_2 > 0 $. Let $ C $ denote the circle $ x^2 + y^2 = 9 $, and $ M $ be the point $ (3, 0) $. Suppose the line $ x = x_1 $ intersects $ C $ at $ R $, and the line $ x = x_2 $ intersects $ C $ at $ S $, such that the $ y $-coordinates of $ R $ and $ S $ are positive. Let $ \angle ROM = \frac{\pi}{6} $ and $ \angle SOM = \frac{\pi}{3} $, where $ O $ denotes the origin $ (0, 0) $. Let $ |XY| $ denote the length of the line segment $ XY $. Then which of the following statements is (are) TRUE?
- JEE Advanced - 2025
- Conic sections
- Adsorption of phenol from its aqueous solution on to fly ash obeys Freundlich isotherm. At a given temperature, from 10 mg g$^{-1}$ and 16 mg g$^{-1}$ aqueous phenol solutions, the concentrations of adsorbed phenol are measured to be 4 mg g$^{-1}$ and 10 mg g$^{-1}$, respectively. At this temperature, the concentration (in mg g$^{-1}$) of adsorbed phenol from 20 mg g$^{-1}$ aqueous solution of phenol will be ____. Use: $\log_{10} 2 = 0.3$
- JEE Advanced - 2025
- Adsorption
- At 300 K, an ideal dilute solution of a macromolecule exerts osmotic pressure that is expressed in terms of the height (h) of the solution (density = 1.00 g cm$^{-3}$) where h is equal to 2.00 cm. If the concentration of the dilute solution of the macromolecule is 2.00 g dm$^{-3}$, the molar mass of the macromolecule is calculated to be $X \times 10^{4}$ g mol$^{-1}$. The value of $X$ is ____. Use: Universal gas constant (R) = 8.3 J K$^{-1}$ mol$^{-1}$ and acceleration due to gravity (g) = 10 m s$^{-2}\}$
- JEE Advanced - 2025
- Colligative Properties
Concepts Used:
Kinetics Equations
It is branch of physics that defines motion with respect to space and time is known as kinematics.
Inverse Kinematics: Inverse Kinematics do the reverse of kinematics.
There are four basic kinematics equations:

Rotational Kinematics Equations
Another branch of kinematics equations which deals with the rotational motion of anybody.
