Find the time required to complete a reaction 90% if the reaction is completed 50% in 15 minutes.
Find the time required to complete a reaction 90% if the reaction is completed 50% in 15 minutes.
Show Hint
Solution and Explanation
Step 1: Determine the order of reaction.
The problem involves percentages of completion and time, which suggests a first-order reaction. The formula for the time required to achieve a certain completion in a first-order reaction is: \[ t = \frac{2.303}{k} \log \frac{[A]_0}{[A]}, \] where: - \( t \) is the time, - \( k \) is the rate constant, - \( [A]_0 \) is the initial concentration, - \( [A] \) is the concentration at time \( t \).
Step 2: Calculate the rate constant \( k \).
For 50\% completion, \( [A]_0/[A] = 2 \). Substituting \( t = 15 \, \text{minutes} \): \[ 15 = \frac{2.303}{k} \log 2. \] \[ k = \frac{2.303 \log 2}{15}. \] Using \( \log 2 = 0.3010 \): \[ k = \frac{2.303 \times 0.3010}{15} = 0.04627 \, \text{min}^{-1}. \]
Step 3: Calculate the time for 90\% completion.
For 90\% completion, \( [A]_0/[A] = 10 \). Substituting into the formula: \[ t = \frac{2.303}{k} \log 10. \] Using \( \log 10 = 1 \): \[ t = \frac{2.303}{0.04627} \times 1. \] \[ t = 49.44 \, \text{minutes}. \]
Step 4: Final Answer.
The time required to complete 90\% of the reaction is: \[ \boxed{49.44 \, \text{minutes}}. \]
Top Questions on kinetics equations
- Magnetic Moment of \( \text{Mn}^{2+} \) is:
- MHT CET - 2024
- Chemistry
- kinetics equations
- IUPAC Name of Glyceraldehyde is:
- MHT CET - 2024
- Chemistry
- kinetics equations
- IUPAC Name of Acetone is:
- MHT CET - 2024
- Chemistry
- kinetics equations
- The half-life period of a first order reaction is 1000 seconds. Its rate constant is:
- KEAM - 2024
- Chemistry
- kinetics equations
- If the distribution of molecular speeds of a gas is as per the figure shown below, then the ratio of the most probable, the average, and the root mean square speeds, respectively, is
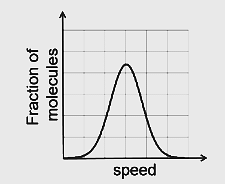
- JEE Advanced - 2020
- Chemistry
- kinetics equations
Questions Asked in MHT CET exam
- How many molecules of carbon dioxide are formed when 0.6 g carbon is burnt in air?
- MHT CET - 2025
- Stoichiometry and Stoichiometric Calculations
- If \( \tan^{-1} (\sqrt{\cos \alpha}) - \cot^{-1} (\cos \alpha) = x \), then what is \( \sin \alpha \)?
- MHT CET - 2025
- Trigonometric Identities
- Given the equation: \[ 81 \sin^2 x + 81 \cos^2 x = 30 \] Find the value of \( x \).
- MHT CET - 2025
- Trigonometric Identities
- Evaluate the integral: \[ \int \frac{1}{\sin^2 2x \cdot \cos^2 2x} \, dx \]
- MHT CET - 2025
- Trigonometric Identities
- What is the frequency of a wave with a wavelength of \( 2 \, \text{m} \) and a velocity of \( 4 \, \text{m/s} \)?
- MHT CET - 2025
- Wave optics