If $A = \frac{1}{3} \begin{bmatrix}1&2&2\\ 2&1&-2\\ a&2&b\end{bmatrix} $ is an orthogonal matrix, then
- a = - 2, b = - 1
- a = 2, b = 1
- a = 2, b = - 1
- a = - 2, b = 1
The Correct Option is A
Solution and Explanation
$\Rightarrow \frac{1}{3} \begin{bmatrix}1&2&2\\ 2&1&-2\\ a&2&b\end{bmatrix} . \frac{1}{3} \begin{bmatrix}1&2&a\\ 2&1&2\\ 2&-2&b\end{bmatrix} = \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix} $
$\Rightarrow \frac{1}{9} \begin{bmatrix}1&2&2\\ 2&1&-2\\ a&2&b\end{bmatrix} \begin{bmatrix}1&2&a\\ 2&1&2\\ 2&-2&b\end{bmatrix} = \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix} $
$\Rightarrow \begin{bmatrix}9&0&a+4+2b\\ 0&9&2a+2-2b\\ a+4+2b&2a+2-2b&a^{2}+4+b^{2}\end{bmatrix} = \begin{bmatrix}9&0&0\\ 0&9&0\\ 0&0&9\end{bmatrix} $
$\Rightarrow a + 4 + 2b = 0, 2a + 2 - 2b = 0 , a^{2} + 4 + b^{2} = 9 $
$\Rightarrow a + 2b + 4 = 0, a - b + 1 = 0 a^{2} + b^{2} = 5 $
$\Rightarrow a = - 2, b = - 1$
Top Questions on Transpose of a Matrix
If the matrix $ A $ is such that $ A \begin{pmatrix} -1 & 2 \\ 3 & 1 \end{pmatrix} = \begin{pmatrix} -4 & 1 \\ 7 & 7 \end{pmatrix} \text{ then } A \text{ is equal to} $
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
If $A = \begin{bmatrix} 5a & -b \\ 3 & 2 \end{bmatrix} \quad \text{and} \quad A \, \text{adj} \, A = A A^t, \quad \text{then} \, 5a + b \, \text{is equal to}$
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
If $3A + 4B^{t} = \left( \begin{array}{cc} 7 & -10 \\ 0 & 6 \end{array} \right) $ and $ 2B - 3A^{t} = \left( \begin{array}{cc} -1 & 18 \\ 4 & -6 \\ -5 & -7 \end{array} \right) $, then find $ (5B)^{t}$:
- COMEDK UGET - 2024
- Mathematics
- Transpose of a Matrix
- If \( A = \begin{bmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix} \), then \( A^{-1} \) is:
- MHT CET - 2024
- Mathematics
- Transpose of a Matrix
- If \[ B = \begin{bmatrix} 3 & \alpha & -1 \\ 1 & 3 & 1 \\ -1 & 1 & 3 \end{bmatrix} \] is the adjoint of a 3x3 matrix \( A \) and \( |A| = 4 \), then \( \alpha \) is equal to:
- MHT CET - 2024
- Mathematics
- Transpose of a Matrix
Questions Asked in BITSAT exam
- A particle moves in a circle of radius 2 m with a speed of 6 m/s. What is the centripetal acceleration of the particle?
- BITSAT - 2025
- Acceleration
- A body of mass 2 kg is moving with a velocity of 10 m/s. What is its kinetic energy?
- BITSAT - 2025
- Mechanics
- A concave mirror produces an image that is real, inverted, and diminished. What is the position of the object in relation to the mirror?
- BITSAT - 2025
- Ray optics and optical instruments
- How much heat is required to raise the temperature of \( 2 \, \text{kg} \) of water from \( 25^\circ C \) to \( 75^\circ C \)? (Specific heat capacity of water \( c = 4200 \, \text{J/kg}^\circ C \))
- BITSAT - 2025
- Thermodynamics
- A particle moves with a constant speed of 4 m/s in a circular path of radius 2 m. What is its centripetal acceleration?
- BITSAT - 2025
- Uniform Circular Motion
Concepts Used:
Transpose of a Matrix
The matrix acquired by interchanging the rows and columns of the parent matrix is called the Transpose matrix. The transpose matrix is also defined as - “A Matrix which is formed by transposing all the rows of a given matrix into columns and vice-versa.”
The transpose matrix of A is represented by A’. It can be better understood by the given example:

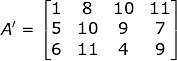
Now, in Matrix A, the number of rows was 4 and the number of columns was 3 but, on taking the transpose of A we acquired A’ having 3 rows and 4 columns. Consequently, the vertical Matrix gets converted into Horizontal Matrix.
Hence, we can say if the matrix before transposing was a vertical matrix, it will be transposed to a horizontal matrix and vice-versa.
Read More: Transpose of a Matrix