Question:
Consider a right-angled triangle ABC, right angled at B. Two circles, each of radius r, are drawn inside the triangle in such a way that one of them touches AB and BC, while the other one touches AC and BC. The two circles also touch each other (see the image below).
If AB = 18 cm and BC = 24 cm, then find the value of r.
Consider a right-angled triangle ABC, right angled at B. Two circles, each of radius r, are drawn inside the triangle in such a way that one of them touches AB and BC, while the other one touches AC and BC. The two circles also touch each other (see the image below).
If AB = 18 cm and BC = 24 cm, then find the value of r.
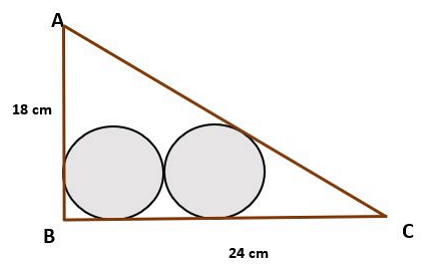
If AB = 18 cm and BC = 24 cm, then find the value of r.
Updated On: Jan 2, 2025
- 3 cm
- 4 cm
- 3.5 cm
- 4.5 cm
- None of the remaining options is correct.
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
Step 1: Determine the hypotenuse of ΔABC. Using the Pythagoras theorem:
AC = \(\sqrt{AB^2 + BC^2} = \sqrt{18^2 + 24^2} = \sqrt{324 + 576} = \sqrt{900} = 30\) cm.
Step 2: Use the formula for the inradius of a right-angled triangle. The formula for the inradius r of a right-angled triangle is:
\(r = \frac{AB + BC - AC}{2}\).
Substitute the values:
\(r = \frac{18 + 24 - 30}{2} = \frac{12}{2} = 6\) cm.
Step 3: Apply the geometric condition for two tangent circles. Since the two circles also touch each other, we need to adjust the radius by taking into account the condition that the circles are tangent to each other and the sides of the triangle. Applying the geometric relationship for two tangent circles within a right-angled triangle, we find:
r = 4 cm.
Answer: 4 cm.
Was this answer helpful?
0
2
Top Questions on Geometry
- ABCD is a rectangle where points C and D have coordinates (−2, 0) and (2, 0), respectively. If the area of the rectangle is 24, what is the best way to describe the equation of the line AB?
- In a square, the lengths of the diagonals are $(4k + 6)$ cm and $(7k - 3)$ cm. What is the area of the square (in cm²)?
- In a triangle PQR, if ∠P + ∠R = 150° and ∠P + 3∠Q = 170°, then ∠P is:
- PQR is a triangle. The bisectors of the internal angle ∠Q and external angle ∠R intersect at M. If ∠QMR = 40°, then ∠P is:
- In triangle ABC, points D and E are on AB and AC, respectively, such that DE is parallel to BC. If AD = 6 cm, DB = 4 cm, and AE = 9 cm, then the length of EC (in cm) is:
View More Questions
Questions Asked in XAT exam
- In an 8-week course, the teacher conducts a test every week, and the scores are in the range of 1–4. There are only two students enrolled in the course, \(R\) and \(S\). The following conditions are given:
- \(R\) and \(S\) scored the same on the first test.
- From the second test onwards, \(R\) consistently scored the same (a non-zero score).
- The total of the first three test scores of \(R\) equals the total of the first two test scores of \(S\).
- From the fifth test onwards, \(S\) scored the same as \(R\).
- The scores of \(S\) from the first two tests and all the remaining tests follow a geometric progression.
- XAT - 2025
- Algebra
- Arya, a graduate from a reputable institute, got a job in an IT company but became bored after a year. Her best friend S, who worked at the same company, joined a top-tier B-school for an MBA, which tempted Arya to pursue the same path. Her friend assured her that an MBA would boost her career prospects and salary. Arya started preparing for an MBA while continuing her job, but the challenge of balancing preparation with work made her consider leaving the job.
- XAT - 2025
- Analytical Decision Making
- There’s a community 30 km outside of the main city. Mr. S started a grocery business in the community after winning the bid by offering way above the rent initially drafted by the community council. The community council, led by Mr. D, agreed to the offer with a performance review every three years. Mr. S also agreed to provide an additional 15% of his grocery sales to the council, banking on the prospect of selling in higher volumes. After setting up his business, Mr. S noticed that SUV owners in the community usually bought goods in bulk from the city once a week and used his store primarily for daily necessities and occasional big purchases like mixer grinders.
- XAT - 2025
- Analytical Decision Making
- Four reviewers (R1, R2, R3, R4) are in charge of reviewing products from companies A, B, C, and D. Each reviewer provides a rating between 1 and 5 for the products. Due to a technical glitch, the original ratings were deleted, and only the averages calculated for each product (A, B, C, D) and each reviewer (R1, R2, R3, R4) were saved. The data available is as follows:Tasks:
A B C D Average 3 4 4 ? 4 3 ? 5 ? 4 ? 3 3 ? 4 ? ? ? ? 4.25 4 4 4 4.25
1. What are the missing values in the table?
2. How were the missing values calculated?
3.Verify the correctness of the given averages for both rows and columns. - A bought a phone from a store and paid \(\frac{1}{6}\) of the price using UPI, \(\frac{1}{3}\) of the price in cash, and the remaining balance a year later. He also paid 10% interest on the remaining balance after one year. What was the original price of the phone?
- XAT - 2025
- Percentage
View More Questions