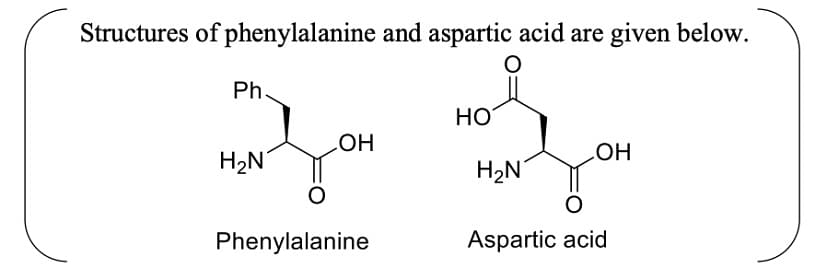
Aspartame, an artificial sweetener, is a dipeptide aspartyl phenylalanine methyl ester. The structure of aspartame is
The Correct Option is B
Approach Solution - 1
Step 1: Understanding Aspartame
Aspartame is a dipeptide formed by the condensation of aspartic acid and phenylalanine. The methyl ester group is added to the carboxyl group of the phenylalanine residue.
Step 2: Structural Features of Aspartame
- Peptide bond: Formed between the carboxyl group of aspartic acid and the amino group of phenylalanine.
- Methyl ester group: Attached to the terminal carboxyl group of phenylalanine.
Step 3: Verifying the Structure
Structure (B) correctly shows the peptide bond between aspartic acid and phenylalanine, with the methyl ester group on phenylalanine.
Conclusion
The correct structure of aspartame is represented by option (B).
Approach Solution -2
To solve the problem, we need to determine the correct structure of aspartame, which is a dipeptide consisting of aspartyl phenylalanine methyl ester.
1. Understanding the Components:
Aspartame is made from aspartic acid and phenylalanine, with the phenylalanine part esterified as a methyl ester.
- Aspartic acid has two carboxyl groups, one of which forms a peptide bond.
- Phenylalanine contains a phenyl (Ph) group attached to the alpha carbon.
2. Structure of Aspartame:
- The amino group of phenylalanine bonds with the carboxyl group of aspartic acid.
- The free carboxyl group of phenylalanine is converted to methyl ester (–COOCH₃).
- The resulting structure is a dipeptide: aspartyl-phenylalanine methyl ester.
3. Identifying the Correct Option:
Among the given options, option (B) correctly shows:
- Aspartic acid with free amino and carboxyl groups.
- Phenylalanine linked via peptide bond.
- Methyl ester group at the carboxyl terminal of phenylalanine.
Thus, option (B) is the correct structure of aspartame.
Final Answer:
Option (B)
Top Questions on Biomolecules
- Which of the following is a polysaccharide?
- CUET (UG) - 2025
- Chemistry
- Biomolecules
- Identify correct conversion during acidic hydrolysis from the following: (A) Starch gives galactose.
(B) Cane sugar gives equal amount of glucose and fructose.
(C) Milk sugar gives glucose and galactose.
(D) Amylopectin gives glucose and fructose.
(E) Amylose gives only glucose.
Choose the correct answer from the options given below:- JEE Main - 2025
- Chemistry
- Biomolecules
Fat soluble vitamins are :
A. Vitamin B\( _1 \)
B. Vitamin C
C. Vitamin E
D. Vitamin B\( _{12} \)
E. Vitamin K
Choose the correct answer from the options given below :- JEE Main - 2025
- Chemistry
- Biomolecules
- Which of the following is the correct structure of L-fructose?
- JEE Main - 2025
- Chemistry
- Biomolecules
- The total number of hydrogen bonds of a DNA-double Helix strand whose one strand has the following sequence of bases is _______ . $5^{\prime}-\mathrm{G}-\mathrm{G}-\mathrm{C}-\mathrm{A}-\mathrm{A}-\mathrm{A}-\mathrm{T}-\mathrm{C}-\mathrm{G}-\mathrm{G}-\mathrm{C}-\mathrm{T}-\mathrm{A}-3^{\prime}$
- JEE Main - 2025
- Chemistry
- Biomolecules
Questions Asked in JEE Advanced exam
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):
- JEE Advanced - 2025
- Waves and Oscillations
- Consider the vectors $$ \vec{x} = \hat{i} + 2\hat{j} + 3\hat{k},\quad \vec{y} = 2\hat{i} + 3\hat{j} + \hat{k},\quad \vec{z} = 3\hat{i} + \hat{j} + 2\hat{k}. $$ For two distinct positive real numbers $ \alpha $ and $ \beta $, define $$ \vec{X} = \alpha \vec{x} + \beta \vec{y} - \vec{z},\quad \vec{Y} = \alpha \vec{y} + \beta \vec{z} - \vec{x},\quad \vec{Z} = \alpha \vec{z} + \beta \vec{x} - \vec{y}. $$ If the vectors $ \vec{X}, \vec{Y}, \vec{Z} $ lie in a plane, then the value of $ \alpha + \beta - 3 $ is ________.
- If $$ \alpha = \int_{\frac{1}{2}}^{2} \frac{\tan^{-1} x}{2x^2 - 3x + 2} \, dx, $$ then the value of $ \sqrt{7} \tan \left( \frac{2\alpha \sqrt{7}}{\pi} \right) $ is.
(Here, the inverse trigonometric function $ \tan^{-1} x $ assumes values in $ \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) $.)- JEE Advanced - 2025
- Integral Calculus
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions