Question

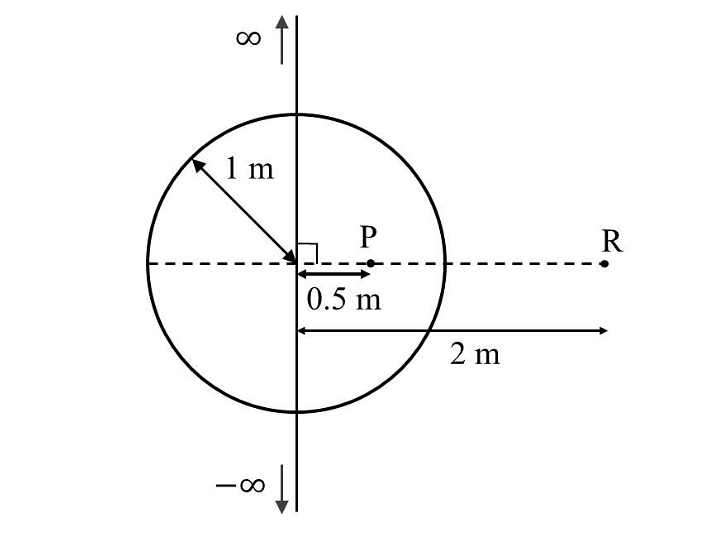
An infinitely long thin wire, having a uniform charge density per unit length of \(5 nC/m,\) is passing through a spherical shell of radius \(1 m\), as shown in the figure. A \(10 nC\) charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points P and R, in Volt, is ______. [Given: In SI units \(\frac{1}{ 4πϵ0} = 9 × 10^9 , ln \ 2 = 0.7\). Ignore the area pierced by the wire.]

Answer 1

Correct Answer: 171

Potential Difference Calculation 

The potential difference is calculated by considering contributions from both a line charge and a sphere charge.

Step 1: Potential Difference Due to the Line Charge

The potential difference due to the line charge is given by: \[ (V_P - V_R)_{\text{line charge}} = 2k \lambda \ln \left( \frac{r_P}{r_R} \right) \] where:

• k: Coulomb’s constant
• \( r_P \): The distance of point P
• \( r_R \): The distance of point R
• \( \lambda \): The linear charge density

Given that: \[ r_P = 126 \, \text{V} \]

Step 2: Potential Difference Due to the Sphere Charge

The potential difference due to the sphere charge is: \[ (V_P - V_R)_{\text{sphere}} = kq \left( \frac{1}{r_R} - \frac{1}{r_R} \right) = kq \cdot \frac{2}{r_R} \] where:

• q: The charge on the sphere
• \( r_R \): The reference radius

Given: \[ (V_P - V_R)_{\text{sphere}} = 45 \, \text{V} \]

Step 3: Total Potential Difference

The total potential difference is: \[ V_P - V_R = 126 + 45 = 171 \, \text{V} \]

Final Answer:

The total potential difference between points P and R is 171 V.

Answer 2

To solve this problem, we need to compute the potential difference between points P and R due to the infinitely long charged wire and the spherical shell with uniformly distributed charge.

Given:

• Linear charge density of the wire: \( \lambda = 5 \, \text{nC/m} = 5 \times 10^{-9} \, \text{C/m} \)
• Total charge on the shell: \( Q = 10 \, \text{nC} = 10 \times 10^{-9} \, \text{C} \)
• Radius of the spherical shell: \( R_s = 1 \, \text{m} \)
• Position of point P: at 0.5 m from wire (inside the shell)
• Position of point R: at 2 m from wire (outside the shell)
• Given constants: \( \frac{1}{4\pi\varepsilon_0} = 9 \times 10^9 \), \( \ln 2 = 0.7 \)

Let’s compute the potential difference \( V_P - V_R \) due to the two charges:

1. Potential due to the spherical shell:
- For a spherical shell, potential inside is constant and equal to the potential on the surface:
\( V_{\text{shell}}(r \leq R_s) = \frac{1}{4\pi\varepsilon_0} \cdot \frac{Q}{R_s} \)
= \( 9 \times 10^9 \cdot \frac{10 \times 10^{-9}}{1} = 90 \, \text{V} \)
So, \( V_P^{\text{(shell)}} = 90 \, \text{V} \) - For point R (outside the shell):
\( V_R^{\text{(shell)}} = \frac{1}{4\pi\varepsilon_0} \cdot \frac{Q}{r} = 9 \times 10^9 \cdot \frac{10 \times 10^{-9}}{2} = 45 \, \text{V} \)

2. Potential due to the infinite wire:
- The potential at a distance \( r \) from an infinitely long line of charge is:
\( V = \frac{\lambda}{2\pi\varepsilon_0} \ln\left( \frac{r_{\text{ref}}}{r} \right) \)
But since we are taking the potential difference \( V_P - V_R \), the reference cancels out and we can write:
\( \Delta V = \frac{\lambda}{2\pi\varepsilon_0} \ln\left( \frac{r_R}{r_P} \right) \)

Substitute values:
- \( r_R = 2 \, \text{m}, \quad r_P = 0.5 \, \text{m} \)
- \( \lambda = 5 \times 10^{-9} \, \text{C/m} \)
- \( \frac{1}{4\pi\varepsilon_0} = 9 \times 10^9 \Rightarrow \frac{1}{2\pi\varepsilon_0} = 18 \times 10^9 \)

\( V_P^{\text{(wire)}} - V_R^{\text{(wire)}} = \lambda \cdot \frac{1}{2\pi\varepsilon_0} \ln\left( \frac{2}{0.5} \right) \)
= \( 5 \times 10^{-9} \cdot 18 \times 10^9 \cdot \ln(4) \)
= \( 90 \cdot \ln(4) \)
But \( \ln(4) = \ln(2^2) = 2 \cdot \ln(2) = 2 \cdot 0.7 = 1.4 \)
So, contribution = \( 90 \cdot 1.4 = 126 \, \text{V} \)

3. Total Potential Difference:
\( V_P - V_R = (V_P^{\text{(shell)}} - V_R^{\text{(shell)}}) + (V_P^{\text{(wire)}} - V_R^{\text{(wire)}}) \)
= \( (90 - 45) + 126 = 45 + 126 = \boxed{171} \, \text{V} \)

Final Answer:
The magnitude of the potential difference between points P and R is 171 V.