$AB$ and $CD$ are $2$ line segments ; where $A(2,3,0),B (6, 9, 0), C(-6, -9, 0). P $ and $Q$ are midpoint of $AB$ and $CD$, respectively and $L$ is the midpoint of $PQ$. Find the distance of $L$ from the plane $3x + 4z + 25 = 0$
- 25
- 15
- 5
- 40
The Correct Option is C
Approach Solution - 1
Using mid-point formula
$Q=\left(\frac{x-6}{2}, \frac{y-9}{2} , \frac{z+0}{2}\right) $
Also, $P=\left(\frac{2+6}{2}, \frac{3+9}{2}, \frac{0+0}{2}\right) =\left(4,6,0\right)$
Since, $AC||PQ$
$ \therefore$ D.r's of line $AC $ = D.r's of line $PQ$
$\Rightarrow \:\: \left(-8 ,12,0\right)=\left(\frac{x-14}{2}, \frac{y-21}{2} , \frac{z}{2}\right) $
$\Rightarrow\:\: x = -2, y = -3, z = 0$
$\Rightarrow\:\:\: D (-2, -3,0) \:\:\: \Rightarrow \:\: Q(-4, - 6,0)$
If $L$ is midpoint of $PQ$ then
$L\left(\frac{4-4}{2}, \frac{6-6}{2}, 0\right)=\left(0,0,0\right)$
$ \therefore$ $ \perp$ distance of $L(0,0,0)$ from the plane $3x + 4z + 25 = 0$ is
$=\left|\frac{3\left(0\right)+4\left(0\right)+25}{\sqrt{\left(3\right)^{2}+\left(4\right)^{2}}}\right|= \left|\frac{25}{\sqrt{25}}\right| =\sqrt{25} =5$
Approach Solution -2
Ans. The word "midpoint" has been used to refer to the exact "center" of anything since the early 14th century. The center point is where the two ends meet. It may also be referred to as the line segment's centroid and its ends.
The midpoint theorem states that "The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side."
The midpoint theorem came to be invented by Rene Descartes, the most popular mathematician of all time. It was a basic geometrical idea at first in Rene’s mind, which represented an ordered pair of numbers. This was later made into a method to help combine arithmetic and geometry. Apart from the cartesian plane, the midpoint has great uses in geometrical figures like triangles, circles, ellipses, hyperbolas, quadrilaterals, and general polygons.
Let’s suppose that a line connects two points (2,6) and (4,2), then the coordinates of the midpoint of the line joining these two points are, [(2+4)/2, (6+2)/2] which gives us (3,4).

Top Questions on Three Dimensional Geometry
- Find the length of the diagonal of a rectangle with length 6 cm and breadth 8 cm.
- MHT CET - 2025
- Mathematics
- Three Dimensional Geometry
- Find the area of a circle whose radius is 7 cm.
- MHT CET - 2025
- Mathematics
- Three Dimensional Geometry
- The area of a triangle with base 12 cm and height 5 cm is?
- MHT CET - 2025
- Mathematics
- Three Dimensional Geometry
- Find the value of λ, if the points A(−1,−1,2), B(2,8,λ), C(3,11,6) are collinear.
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
- The angle between the planes \(2x-y+z=6\) and \(x+y+2z=7\) is:
- VITEEE - 2025
- Mathematics
- Three Dimensional Geometry
Questions Asked in COMEDK UGET exam
- Given that the freezing point of benzene is $ 5.48^\circ C $ and its $ K_f $ value is $ 5.12^\circ C/m $, what would be the freezing point of a solution of 20 g of propane in 400 g of benzene?
- COMEDK UGET - 2024
- Colligative Properties
200 ml of an aqueous solution contains 3.6 g of Glucose and 1.2 g of Urea maintained at a temperature equal to 27$^{\circ}$C. What is the Osmotic pressure of the solution in atmosphere units?
Given Data R = 0.082 L atm K$^{-1}$ mol$^{-1}$
Molecular Formula: Glucose = C$_6$H$_{12}$O$_6$, Urea = NH$_2$CONH$_2$- COMEDK UGET - 2024
- Colligative Properties
- An inorganic compound W undergoes the following reactions: $ W + \text{Na}_2\text{CO}_3 \xrightarrow{\text{O}_2 / \text{heat}} X + H^+ \xrightarrow{} Y(s) $ $ Y(aq) + \text{KCl} (aq) \xrightarrow{} Z(s) $ Z appears in the form of orange crystals and is used as an oxidising agent in acid medium. Identify the compound W.
- COMEDK UGET - 2024
- coordination compounds
- A current of 3.0 A is passed through 750 ml of 0.45 M solution of CuSO₄ for 2 hours with a current efficiency of 90\%. If the volume of the solution is assumed to remain constant, what would be the final molarity of CuSO₄ solution?
- COMEDK UGET - 2024
- Solutions
- For a reaction $ 5X + Y \to 3Z $, the rate of formation of Z is $ 2.4 \times 10^{-5} \, \text{mol L}^{-1} \text{s}^{-1} $. Calculate the average rate of disappearance of X.
- COMEDK UGET - 2024
- Stoichiometry and Stoichiometric Calculations
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
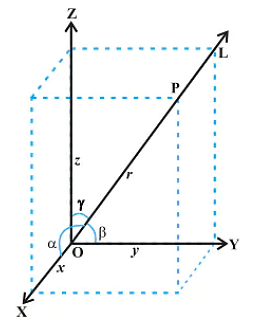
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.