Question:
A wave on a string meets with another wave producing a node at . Then the equation of the unknown wave is:
A wave on a string meets with another wave producing a node at . Then the equation of the unknown wave is:
Updated On: Sep 1, 2025
- (A)
- (B)
- (C)
- (D)
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
Explanation:
Given:Equation of wave, ......(i)Since the coefficient of is negative in the above wave equation, it suggests that the wave is traveling in a positive direction. The other wave must travel in the opposite direction to form a node.Let the two possible equations of waves travelling in negative direction be......(ii)and.......(iii)Using the propertyIf waves (i) and (ii) superimpose, the net displacement isSimilarly,So, if waves (i) and (iii) superimpose the net displacement isSince at node, displacement so Therefore, eq. (iii) satisfies the property of a node at .So, the equation of the unknown wave isHence, the correct option is (B).
Given:Equation of wave, ......(i)Since the coefficient of is negative in the above wave equation, it suggests that the wave is traveling in a positive direction. The other wave must travel in the opposite direction to form a node.Let the two possible equations of waves travelling in negative direction be......(ii)and.......(iii)Using the propertyIf waves (i) and (ii) superimpose, the net displacement isSimilarly,So, if waves (i) and (iii) superimpose the net displacement isSince at node, displacement so Therefore, eq. (iii) satisfies the property of a node at .So, the equation of the unknown wave isHence, the correct option is (B).
Was this answer helpful?
0
0
Top Questions on Amperes circuital law
- A coil has a resistance of \( 30 \, \Omega \) and an inductive reactance of \( 20 \, \Omega \) at 50 Hz frequency. If an AC source of 200 V and 100 Hz is connected across the coil, then how much current will flow through the coil?
- MHT CET - 2024
- Physics
- Amperes circuital law
- In a series LCR circuit connected to an AC source, at resonance, the current is maximum because:
- MHT CET - 2024
- Physics
- Amperes circuital law
Consider the circuit shown :
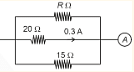 The ammeter reads 0.9 A. Value of R is
The ammeter reads 0.9 A. Value of R is- JEE Main - 2024
- Physics
- Amperes circuital law
- Among the following, Ampere’s circuital law is represented by:
- AP EAPCET - 2023
- Physics
- Amperes circuital law
- In the given circuit, find the voltage drop VL in the load resistance RL

- WBJEE - 2023
- Physics
- Amperes circuital law
View More Questions
Questions Asked in JEE Main exam
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- The area of the region enclosed by the curves \( y = x^2 - 4x + 4 \) and \( y^2 = 16 - 8x \) is:
- JEE Main - 2025
- Area between Two Curves
- 2.8 \( \times 10^{-3} \) mol of \( \text{CO}_2 \) is left after removing \( 10^{21} \) molecules from its ‘\( x \)’ mg sample. The mass of \( \text{CO}_2 \) taken initially is: Given: \( N_A = 6.02 \times 10^{23} \, \text{mol}^{-1} \)
- JEE Main - 2025
- Mole concept and Molar Masses
- A conducting bar moves on two conducting rails as shown in the figure. A constant magnetic field \( B \) exists into the page. The bar starts to move from the vertex at time \( t = 0 \) with a constant velocity. If the induced EMF is \( E \propto t^n \), then the value of \( n \) is ________________________.

- JEE Main - 2025
- Electromagnetic induction

In the first configuration (1) as shown in the figure, four identical charges \( q_0 \) are kept at the corners A, B, C and D of square of side length \( a \). In the second configuration (2), the same charges are shifted to mid points C, E, H, and F of the square. If \( K = \frac{1}{4\pi \epsilon_0} \), the difference between the potential energies of configuration (2) and (1) is given by:
- JEE Main - 2025
- Electromagnetic Field (EMF)
View More Questions