A student needs to prepare a buffer solution of propanoic acid and its sodium salt with pH 4. The ratio of
\(\frac{[CH_3CH_2COO^−]}{[CH_3CH_2COOH] }\)
required to make buffer is _____.
Given : Ka(CH3CH2COOH) = 1.3 × 10–5
A student needs to prepare a buffer solution of propanoic acid and its sodium salt with pH 4. The ratio of
\(\frac{[CH_3CH_2COO^−]}{[CH_3CH_2COOH] }\)
required to make buffer is _____.
Given : Ka(CH3CH2COOH) = 1.3 × 10–5
0.03
0.13
0.23
0.33
The Correct Option is B
Solution and Explanation
The correct answer is (B) : 0.13
\(CH_3CH_2COOH⇌CH_3CH_2COO^−+H^+\)
From Henderson equation
\(pH=pK_a+log\frac{[CH_3CH_2COO^−]}{[CH_3CH_2COOH]}\)
\(4=−log 1.3×10^{−5} log\frac{[CH_3CH_2COO^−]}{[CH_3CH_2COOH]}\)
\(−log^{10^{−4}}=−log1.3×10^{−5}+log\frac{[CH_3CH_2COO^−]}{[CH_3CH_2COOH]}\)
\(−log^{10^{−4}}=−log1.3×10^{−5} \frac{[CH_3CH_2COOH]}{[CH_3CH_2COO^-]}\)
\(10^{−4}=1.3×10^{−5}\frac{[CH_3CH_2COOH]}{[CH_3CH_2COO^-]}\)
\(\frac{[CH_3CH_2COO^−]}{[CH_3CH_2COOH]}=0.13\)
Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant
- What is the pH of 0.365% (w/V) HCl aqueous solution? (HCl=36.5 u), (log 0.365=−0.4377)
- TS EAMCET - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- Given $K_p$ for $2AO_2 + O_2 \rightleftharpoons 2AO_3$ is $4 \times 10^{10}$. Find $K_p'$ for $3AO_3 \rightleftharpoons 3AO_2 + \frac{3}{2} O_2$.
- TS EAMCET - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- Higher yield of NO in the reaction
N$_2$ (g) + O$_2$ (g) $\rightarrow$ 2NO (g)
can be obtained at [$\Delta H$ of the reaction = +180.7 kJ mol$^{-1}$]- NEET (UG) - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
For the reaction A(g) $\rightleftharpoons$ 2B(g), the backward reaction rate constant is higher than the forward reaction rate constant by a factor of 2500, at 1000 K.
[Given: R = 0.0831 atm $mol^{–1} K^{–1}$]
$K_p$ for the reaction at 1000 K is:- NEET (UG) - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- For the reaction $ N_2 + 3H_2 \rightleftharpoons 2NH_3 $, if initially 1 mole of $ N_2 $ and 3 moles of $ H_2 $ are taken and at equilibrium 0.4 moles of $ NH_3 $ are formed, find the equilibrium concentration of $ H_2 $.
- BITSAT - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
Questions Asked in JEE Main exam
Let $ A \in \mathbb{R} $ be a matrix of order 3x3 such that $$ \det(A) = -4 \quad \text{and} \quad A + I = \left[ \begin{array}{ccc} 1 & 1 & 1 \\2 & 0 & 1 \\4 & 1 & 2 \end{array} \right] $$ where $ I $ is the identity matrix of order 3. If $ \det( (A + I) \cdot \text{adj}(A + I)) $ is $ 2^m $, then $ m $ is equal to:
- JEE Main - 2025
- Determinants
- An air bubble of radius 0.1 cm lies at a depth of 20 cm below the free surface of a liquid of density 1000 kg/m\(^3\). If the pressure inside the bubble is 2100 N/m\(^2\) greater than the atmospheric pressure, then the surface tension of the liquid in SI units is (use \(g = 10 \, {m/s}^2\)).
- JEE Main - 2025
- Surface Tension
- A force of 49 N acts tangentially at the highest point of a sphere (solid of mass 20 kg) kept on a rough horizontal plane. If the sphere rolls without slipping, then the acceleration of the center of the sphere is:
- JEE Main - 2025
- Quantum Mechanics
- Let a circle C pass through the points (4, 2) and (0, 2), and its centre lie on \(3x + 2y + 2 = 0\). Then the length of the chord of the circle C, whose midpoint is (1, 2), is:
- JEE Main - 2025
- Coordinate Geometry
A square loop of sides \( a = 1 \, {m} \) is held normally in front of a point charge \( q = 1 \, {C} \). The flux of the electric field through the shaded region is \( \frac{5}{p} \times \frac{1}{\varepsilon_0} \, {Nm}^2/{C} \), where the value of \( p \) is:

- JEE Main - 2025
- Gauss's Law
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
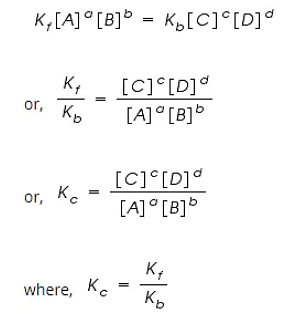
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.