Question

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.

Answer 1

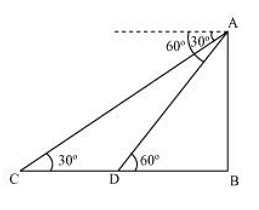
Initial position of the car is C, which changes to D after six seconds. 

In ∆ADB, 

\(\frac{AB}{ DB} = tan 60^{\degree}\)

\(\frac{AB}{ DB} = \sqrt3\)

\(DB = \frac{AB} { \sqrt3}\)

In ∆ABC, 

\(\frac{AB}{ BC}= tan 30^{\degree}\)

\(\frac{ AB }{ BD + DC} = \frac1{ \sqrt3}\)

\(AB \sqrt3 = BD + DC \)

\( AB \sqrt3 = \frac{AB }{\sqrt3} + DC\)

\( DC = AB \sqrt3 -\frac{ AB}{ \sqrt3} = AB (\sqrt3- \frac{1}{ \sqrt3})\)

\(\)\(DC= \frac{2AB}{ \sqrt3}\)

Time taken by the car to travel distance DC= (i.e., \(\frac{2AB}{ \sqrt3}\)) = 6 seconds 

Time taken by the car to travel distance DB (i.e., \(\frac{AB}{ \sqrt3}\) ) = \(\frac{6}{\frac{ 2AB}{ \sqrt3}} \times \frac{AB}{ \sqrt3}\) = \(\frac 6{2}\) = 3 seconds.