Question

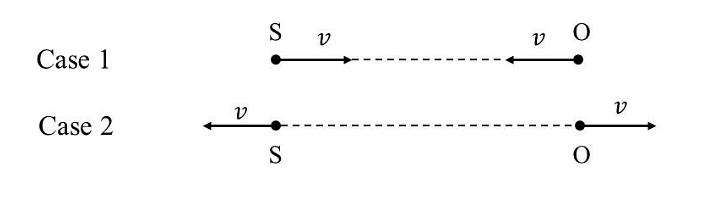
A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.

Answer 1

Correct Answer: 200

To solve the problem, we need to find the observed frequency when the observer and the source move away from each other.

1. Given Data:
The original frequency of the source is $f_0 = 240 \, \text{Hz}$.
The speed of the observer and the source with respect to the ground is $v$.
The speed of sound in air is $V$.

2. Case 1 - Moving Towards Each Other:
In Case 1, the observer and the source move towards each other, so the observed frequency is:

$ f_1 = f_0 \frac{V+v}{V-v} = 288 \, \text{Hz}$

3. Solving for $v$:
We have:

$ \frac{V+v}{V-v} = \frac{288}{240} = \frac{6}{5}$
Multiplying both sides by $5(V-v)$ gives:

$ 5(V+v) = 6(V-v)$
Expanding the terms gives:

$ 5V + 5v = 6V - 6v$
Combining like terms:

$ 11v = V$
Therefore, $v = \frac{V}{11}$.

4. Case 2 - Moving Away From Each Other:
In Case 2, the observer and the source move away from each other, so the observed frequency is:

$ f_2 = f_0 \frac{V-v}{V+v} = n \, \text{Hz}$

5. Substituting $v = \frac{V}{11}$ into the Formula:
We have:

$ n = 240 \frac{V - \frac{V}{11}}{V + \frac{V}{11}}$
This simplifies to:

$ n = 240 \frac{\frac{10V}{11}}{\frac{12V}{11}} = 240 \times \frac{10}{12} = 240 \times \frac{5}{6} = 200$

Final Answer:
The final answer is $\boxed{200}$.

Answer 2

To solve this Doppler effect problem, we use the formulas for frequency observed when the source and observer move towards and away from each other.

Given:
- Source frequency \( f = 240 \, \text{Hz} \)
- Observed frequency when moving towards each other \( f' = 288 \, \text{Hz} \)
- Observed frequency when moving away \( f'' = n \, \text{Hz} \) (to be found)
- Speed of sound in air \( v_s \) (assumed constant)
- Speed of source and observer relative to ground = \( v \)

Step 1: Doppler effect formula
When source and observer move towards each other with speed \( v \):
\[ f' = f \frac{v_s + v}{v_s - v} \] When source and observer move away from each other with speed \( v \):
\[ f'' = f \frac{v_s - v}{v_s + v} \]

Step 2: Use the given values to find \( v_s \) and \( v \)
From the towards case:
\[ 288 = 240 \cdot \frac{v_s + v}{v_s - v} \] Simplify:
\[ \frac{288}{240} = 1.2 = \frac{v_s + v}{v_s - v} \] Cross-multiplied:
\[ 1.2 (v_s - v) = v_s + v \] \[ 1.2 v_s - 1.2 v = v_s + v \] \[ 1.2 v_s - v_s = v + 1.2 v \] \[ 0.2 v_s = 2.2 v \] \[ v = \frac{0.2}{2.2} v_s = \frac{1}{11} v_s \]

Step 3: Find \( n = f'' \)
Using the away formula:
\[ n = 240 \times \frac{v_s - v}{v_s + v} = 240 \times \frac{1 - \frac{1}{11}}{1 + \frac{1}{11}} = 240 \times \frac{\frac{10}{11}}{\frac{12}{11}} = 240 \times \frac{10}{12} = 240 \times \frac{5}{6} = 200 \]

Final Answer:
\[ \boxed{n = 200 \text{ Hz}} \]