Question:
A car P travelling at 20 \(ms^{–1}\) sounds its horn at a frequency of 400 Hz. Another car Q is travelling being the first car in the same direction with a velocity 40 \(ms^{–1}\) . The frequency heard by the passenger of the car Q is approximately [Take, velocity of sound = 360 \(ms^{–1}\) ]
A car P travelling at 20 \(ms^{–1}\) sounds its horn at a frequency of 400 Hz. Another car Q is travelling being the first car in the same direction with a velocity 40 \(ms^{–1}\) . The frequency heard by the passenger of the car Q is approximately [Take, velocity of sound = 360 \(ms^{–1}\) ]
Updated On: Mar 4, 2024
- 485 Hz
- 421 Hz
- 471 Hz
- 514 Hz
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The Correct Option is (B):421 Hz
Was this answer helpful?
0
0
Top Questions on doppler effect
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
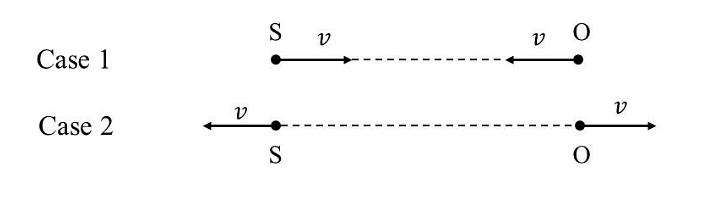
- JEE Advanced - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
A source of sound is moving away from a stationary observer with constant velocity 40 m/s. Find frequency heard by observer, if original frequency of source is 400 Hz and speed of sound in air is 360 m/s
- JEE Main - 2023
- Physics
- doppler effect
- S1 & S2 are sources of the sound of frequency 656 Hz. S1 is moving along OP and S2 is moving on the circle in an anticlockwise direction with a constant speed of 4√2 m\s. P is a detector that is fixed. Select the correct options (Vsound=300m\s)
- JEE Advanced - 2023
- Physics
- doppler effect
- speeds of $20\, m/s$ and $15\, m/s$ relative to the ground. The first train sounds a whistle of frequency $600\, Hz$. The frequency of the whistle heard by a passenger in the second train before the train meets, is (the speed of sound in air is 340 m/s)
- BITSAT - 2019
- Physics
- doppler effect
View More Questions
Questions Asked in JEE Main exam
- Let \[ \vec{a} = 2\hat{i} + \alpha \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} + \hat{k}, \quad \vec{c} = \beta \hat{j} - \hat{k}, \] where \( \alpha \) and \( \beta \) are integers and \( \alpha \beta = -6 \). Let the values of the ordered pair \( (\alpha, \beta) \) for which the area of the parallelogram of diagonals \( \vec{a} + \vec{b} \) and \( \vec{b} + \vec{c} \) is \( \frac{\sqrt{21}}{2} \), be \( (\alpha_1, \beta_1) \) and \( (\alpha_2, \beta_2) \). Then \( \alpha_1^2 + \beta_1^2 - \alpha_2 \beta_2 \) is equal to:
- JEE Main - 2024
- Vectors
- The molecular formula of second homologue in the homologous series of monocarboxylic acid is
- JEE Main - 2024
- Aldehydes, Ketones and Carboxylic Acids
- Given below are two statements: Statement I: $\text{PF}_5$ and $\text{BrF}_5$ both exhibit $\text{sp}^3\text{d}$ hybridisation.Statement II: Both $\text{SF}_6$ and $[\text{Co}(\text{NH}_3)_6]^{3+}$ exhibit $\text{sp}^3\text{d}^2$ hybridisation. In the light of the above statements,choose the correct answer from the options given below:
- JEE Main - 2024
- Hybridisation
- Consider the system of linear equations \( x + y + z = 4\mu \), \( x + 2y + 2\lambda z = 10\mu \), \( x + 3y + 4\lambda^2 z = \mu^2 + 15 \), where \( \lambda, \mu \in \mathbb{R} \). Which one of the following statements is NOT correct?
- JEE Main - 2024
- Linear Algebra
- If the constant term in the expansion of \((1 + 2x - 3x^3) \left(\frac{3}{2}x^2 - \frac{1}{3x}\right)^9\) is \( p \), then \( 108p \) is equal to _________.
- JEE Main - 2024
- Algebra
View More Questions