Question:
When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
When both the source of sound and observer approach each other with a speed equal to 10% of the speed of sound, then the percentage change in frequency heard by the observer is nearly
Show Hint
When both source and observer move towards each other, Doppler effect frequency shift is calculated by \(\frac{v + v_o}{v - v_s}\).
Updated On: Jun 4, 2025
- 33.3%
- 12.2%
- 22.2%
- 11.1%
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Using Doppler effect formula for both source and observer moving towards each other with speed \(v_s = v_o = 0.1v\), where \(v\) is speed of sound: \[ f' = f \times \frac{v + v_o}{v - v_s} = f \times \frac{v + 0.1v}{v - 0.1v} = f \times \frac{1.1v}{0.9v} = 1.222 f \] Percentage change in frequency: \[ (1.222 - 1) \times 100 = 22.2% \]
Was this answer helpful?
0
0
Top Questions on doppler effect
- A passenger is sitting in a fast moving train. The engine of the train blows a whistle of frequency N. If the apparent frequency of sound heard by the passengers is \( N' \), then:
- MHT CET - 2025
- Physics
- doppler effect
- A source (S) of sound has frequency\( 240 Hz\). When the observer (O) and the source move towards each other at a speed \(v\) with respect to the ground (as shown in Case 1 in the figure), the observer measures the frequency of the sound to be \(288 Hz\). However, when the observer and the source move away from each other at the same speed v with respect to the ground (as shown in Case 2 in the figure), the observer measures the frequency of sound to be \(n\) Hz. The value of \(n\) is _____.
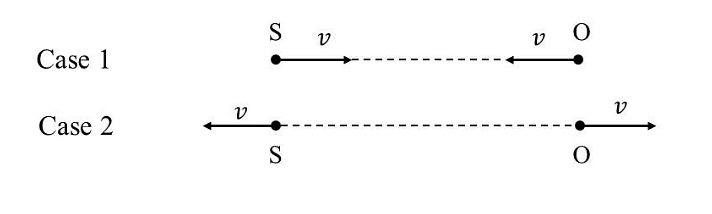
- JEE Advanced - 2024
- Physics
- doppler effect
- A galaxy is moving away from the Earth so that a spectral line at 6000 Å is observed at 6300 Å. Then the speed of the galaxy with respect to the Earth is
- KCET - 2024
- Physics
- doppler effect
- A train is moving with a speed of \(10 m/s\) towards a platform and blows a horn with frequency \(400 Hz\). Find the frequency heard by a passenger standing on the platform. Take speed of sound = \(310 m/s\).
- JEE Main - 2023
- Physics
- doppler effect
- A car P travelling at 20 \(ms^{–1}\) sounds its horn at a frequency of 400 Hz. Another car Q is travelling being the first car in the same direction with a velocity 40 \(ms^{–1}\) . The frequency heard by the passenger of the car Q is approximately [Take, velocity of sound = 360 \(ms^{–1}\) ]
- JEE Main - 2023
- Physics
- doppler effect
View More Questions
Questions Asked in AP EAPCET exam
- In a series LCR circuit, the voltages across the capacitor, resistor, and inductor are in the ratio 2:3:6. If the voltage of the source in the circuit is 240 V, then the voltage across the inductor is
- AP EAPCET - 2025
- Electromagnetic induction
- 0.25 moles of $ \text{CH}_2\text{FCOOH} $ was dissolved in $ 0.5 \, \text{kg} $ of water. The depression in freezing point of the resultant solution was observed as $ 1^\circ \text{C} $. What is the van't Hoff factor? ($ K_f = 1.86 \, \text{K kg mol}^{-1} $)
- AP EAPCET - 2025
- Colligative Properties
- At $T(K)$, the vapor pressure of water is $x$ kPa. What is the vapor pressure (in kPa) of 1 molal solution containing non-volatile solute?
- AP EAPCET - 2025
- Colligative Properties
- At 300 K, vapour pressure of pure liquid A is 70 mm Hg. It forms an ideal solution with liquid B. Mole fraction of B = 0.2 and total vapour pressure of solution = 84 mm Hg. What is vapour pressure (in mm) of pure B?
- AP EAPCET - 2025
- Colligative Properties
- A 1% (w/v) aqueous solution of a certain solute is isotonic with a 3% (w/v) solution of glucose (molar mass 180 g mol$^{-1}$). The molar mass of solute (in g mol$^{-1}$) is
- AP EAPCET - 2025
- Colligative Properties
View More Questions