A parallel beam of light is allowed to fall on a transparent spherical globe of diameter 30 cm and refractive index 1.5. The distance from the centre of the globe at which the beam of light can converge is________ mm.
Correct Answer: 225
Solution and Explanation
The correct answer is: 225
1st refraction:
\(\frac{1.5}{V_1}-0=\frac{0.5}{15}\)
\(⇒ v_1 = 45 \)cm
2nd refraction:
\(\frac{1}{v_2}-\frac{1.5}{15}=\frac{-0.5}{-15}\)
\(⇒ \frac{1}{v_2}=\frac{1}{30}+\frac{1}{10}\)
\(⇒ v2 = +7.5 \)cm
\(⇒\) Distance from centre = 22.5 cm
Top Questions on Units and measurement
- A car travels at a speed of $ 72 \, \text{km/h} $. What is the car's speed in meters per second?
- MHT CET - 2025
- Physics
- Units and measurement
- The mass of an object is measured as \( (28 \pm 0.01) \) g and its volume as \( (5 \pm 0.1) \) cm\(^3\). What is the percentage error in density?
- MHT CET - 2025
- Physics
- Units and measurement
Mass = \( (28 \pm 0.01) \, \text{g} \), Volume = \( (5 \pm 0.1) \, \text{cm}^3 \). What is the percentage error in density?
- MHT CET - 2025
- Physics
- Units and measurement
- A tiny metallic rectangular sheet has length and breadth of 5 mm and 2.5 mm, respectively. Using a specially designed screw gauge which has pitch of 0.75 mm and 15 divisions in the circular scale, you are asked to find the area of the sheet. In this measurement, the maximum fractional error will be \( \frac{x}{100} \), where \( x \) is:
- JEE Main - 2025
- Physics
- Units and measurement
- What are the units of viscosity, intensity of wave, and pressure gradient?
- JEE Main - 2025
- Chemistry
- Units and measurement
Questions Asked in JEE Main exam
The remainder when \( 64^{64} \) is divided by 7 is equal to:
- JEE Main - 2025
- Arithmetic Progression
- The sum of the infinite series $ \cot^{-1} \left( \frac{7}{4} \right) + \cot^{-1} \left( \frac{19}{4} \right) + \cot^{-1} \left( \frac{39}{4} \right) + \cot^{-1} \left( \frac{67}{4} \right) + ... $ is:
- JEE Main - 2025
- Sequence and series
- If $ \alpha $ is a root of the equation $ x^2 + x + 1 = 0 $ and $$ \sum_{k=1}^{n} \left( \alpha^k + \frac{1}{\alpha^k} \right)^2 = 20$$, then n is equal to _______
- JEE Main - 2025
- Sequence and series
x mg of Mg(OH)$_2$ (molar mass = 58) is required to be dissolved in 1.0 L of water to produce a pH of 10.0 at 298 K. The value of x is ____ mg. (Nearest integer) (Given: Mg(OH)$_2$ is assumed to dissociate completely in H$_2$O)
- JEE Main - 2025
- Equilibrium
- The amount of calcium oxide produced on heating 150 kg limestone (75% pure) is _______ kg. (Nearest integer)
Given: Molar mass (in g mol$^{-1}$) of Ca-40, O-16, C-12- JEE Main - 2025
- Stoichiometry and Stoichiometric Calculations
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
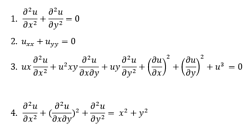
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
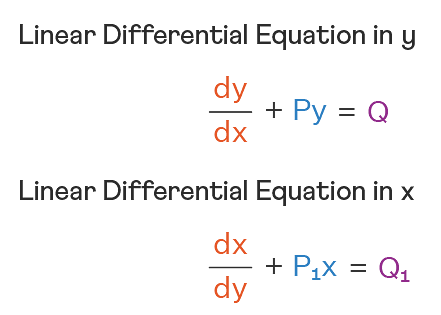
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations