Question

A massless square loop, of wire of resistance $10\, \Omega$, supporting a mass of $1 \, g$, hangs vertically with one of its sides in a uniform magnetic field of $10^3 G$, directed outwards in the shaded region A de voltage $V$ is applied to the loop For what value of $V$, the magnetic force will exactly balance the weight of the supporting mass of $1 g$ ?(If sides of the loop $=10 \, cm , g =10\, ms ^{-2}$ )

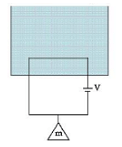
• A. $\frac{1}{10} V$
• B. $1 V$
• C. $100 V$ $
• D. 10 V$

Answer 1

The Correct Option is D

The relationship between the charges and radii is given by: 

\[ \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q_1'}{R} = \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q_2'}{2R} \]

Simplifying, we find:

\[ Q_2' = 2Q_1' \]

Using the charge conservation equation:

\[ Q_1' + Q_2' = Q_1 + Q_2 \]

Substitute \(Q_2' = 2Q_1'\):

\[ Q_1' + 2Q_1' = 20 \pi R^2 \sigma \]

\[ 3Q_1' = 20 \pi R^2 \sigma \]

\[ Q_1' = \frac{20 \pi R^2 \sigma}{3} \]

Substitute \(Q_2' = 2Q_1'\):

\[ Q_2' = \frac{40 \pi R^2 \sigma}{3} \]

The surface charge densities are related by:

\[ \sigma' = \frac{Q_2'}{4 \pi (2R)^2} \]

\[ \sigma' = \frac{\frac{40 \pi R^2 \sigma}{3}}{16 \pi R^2} \]

\[ \sigma' = \frac{40}{3} \cdot \frac{1}{16} \cdot \sigma \]

\[ \sigma' = \frac{5}{6} \cdot \sigma \]

Electromagnetic Force and Voltage:

The force on a current-carrying conductor in a magnetic field is given by:

\[ F_m = ILB \]

Equating with gravitational force \(F_m = mg\):

\[ ILB = mg \]

Substitute \(I = \frac{V}{R}\):

\[ \left(\frac{V}{R}\right)LB = mg \]

Solve for \(V\):

\[ V = \frac{mgR}{LB} \]

Substitute the given values \(m = 1 \times 10^{-3} \ \text{kg}\), \(g = 10 \ \text{m/s}^2\), \(R = 10 \ \Omega\), \(L = 0.1 \ \text{m}\), and \(B = 10^{-3} \ \text{T}\):

\[ V = \frac{(1 \times 10^{-3})(10)(10)}{(0.1)(10^{-3})} \]

\[ V = 10 \ \text{V} \]

Final Answer:

Voltage \(V = 10 \ \text{V}\)