A long straight wire with a circular cross-section having radius R, is carrying a steady current I. The current I is uniformly distributed across this cross-section. Then the variation of magnetic field due to current I with distance r (r < R) from its centre
- \(B∝r^2\)
- \(B∝r\)
- \(B∝\frac {1}{r^2}\)
- \(B∝\frac {1}{r}\)
The Correct Option is B
Solution and Explanation
We know that,
\(∫B.dl = μ_0l_{in}\)
\(B \times 2\pi r = \frac {μ_0l}{\pi R^2} \times \pi r^2\)
\(⇒ B ∝ r\)
So, the correct option is (B): \(B ∝ r\)
Top Questions on Amperes circuital law
Consider the circuit shown :
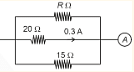The ammeter reads 0.9 A. Value of R is- JEE Main - 2024
- Physics
- Amperes circuital law
- In the given circuit, find the voltage drop VL in the load resistance RL
- WBJEE - 2023
- Physics
- Amperes circuital law
- A transistor is used in an amplifier circuit in common emitter mode. If the base current changes by 100μA, it brings a change of 10mA in collector current. If the load resistance is 2kΩ and input resistance is 1kΩ, the value of power gain is \(x×10^4\). The value of x is _______.
- JEE Main - 2022
- Physics
- Amperes circuital law
- A thick current carrying cable of radius $'R'$ carries current $'I'$ uniformly distributed across its cross-section. The variation of magnetic field $B ( r )$ due to the cable with the distance $'r'$ from the axis of the cable is represented by :
- NEET (UG) - 2021
- Physics
- Amperes circuital law
- Which o f the following is true with respect to Rogers spiral experiment?
- JKCET - 2019
- Physics
- Amperes circuital law
Questions Asked in JEE Main exam
- The de-Broglie wavelength associated with a particle of mass \( m \) and energy \( E \) is \[\lambda = \frac{h}{\sqrt{2mE}}.\]The dimensional formula for Planck's constant is:
- JEE Main - 2024
- de broglie hypothesis
- If the foci of a hyperbola are the same as that of the ellipse \( \frac{x^2}{9} + \frac{y^2}{25} = 1 \) and the eccentricity of the hyperbola is \( \frac{15}{8} \) times the eccentricity of the ellipse,then the smaller focal distance of the point \( \left( \sqrt{2}, \frac{14}{3} \sqrt{5} \right) \) on the hyperbola, is equal to
- JEE Main - 2024
- Coordinate Geometry
- Two wires A and B are made up of the same material and have the same mass. Wire A has radius \(2.0 \, \text{mm}\) and wire B has radius \(4.0 \, \text{mm}\). The resistance of wire B is \(2 \, \Omega\). The resistance of wire A is _____ \( \Omega \).
- JEE Main - 2024
- Resistance
- A convex lens of focal length 40 cm forms an image of an extended source of light on a photo-electric cell. A current \( I \) is produced. The lens is replaced by another convex lens having the same diameter but focal length 20 cm. The photoelectric current now is:
- JEE Main - 2024
- Dual nature of matter
- For a sparingly soluble salt \( \text{AB}_2 \), the equilibrium concentrations of \( \text{A}^{2+} \) ions and \( \text{B}^- \) ions are \( 1.2 \times 10^{-4} \, \text{M} \) and \( 0.24 \times 10^{-3} \, \text{M} \), respectively. The solubility product of \( \text{AB}_2 \) is:
- JEE Main - 2024
- Method of Preparation of Diazoniun Salts
Concepts Used:
Amperes circuital law
According to Ampere’s law, magnetic fields are related to the electric current that is produced in them. This law specifies that the magnetic field is associated with a given current or vice-versa, provided that the electric field doesn’t change with time.
Ampere’s circuital law can be written as the line integral of the magnetic field surrounding the closed loop which is equal to the number of times the algebraic sum of currents passing through the loop.
According to the second equation, if the magnetic field is integrated along the blue path, then it is equal to the current enclosed, I.
The magnetic field doesn’t vary at a distance r because of symmetry. The path length (in blue) in figure 1 has to be equal to the circumference of a circle,2πr.
