Question:
A conducting square loop of side L and resistance R moves in its plane with a uniform velocity v, perpendicular to one of its sides. A magnetic field of induction B, constant in space and time and pointing perpendicularly into the plane of the square, exists everywhere in space. The current induced in the loop is
A conducting square loop of side L and resistance R moves in its plane with a uniform velocity v, perpendicular to one of its sides. A magnetic field of induction B, constant in space and time and pointing perpendicularly into the plane of the square, exists everywhere in space. The current induced in the loop is
Updated On: Jul 27, 2022
- BLv/R in the clockwise direction
- BLv/R in the anticlockwise direction
- 2 BLv/R in the clockwise direction
- zero
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
From Faraday's law of electromagnetic induction, emf is induced with changing magnetic flux, but in this case since, magnetic field is pointing perpendicularly hence, magnetic flux does not change, hence current in the loop is zero.
Was this answer helpful?
0
0
Top Questions on Faradays laws of induction
- In a coil, the current changes form –2 A to +2A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is :
- JEE Main - 2024
- Physics
- Faradays laws of induction
- The magnetic flux \(\phi\) (in weber) linked with a closed circuit of resistance \(8 \, \Omega\) varies with time (in seconds) as \(\phi = 5t^2 - 36t + 1\). The induced current in the circuit at \(t = 2 \, \text{s}\) is ______ A.
- JEE Main - 2024
- Physics
- Faradays laws of induction
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Physics
- Faradays laws of induction
- A square loop of side 2 cm enters a magnetic field with a constant speed of 2 cm s-1 as shown. The front edge enters the field at t = 0s. Which of the following graph correctly depicts the induced emf in the loop?
( Take clockwise direction positive )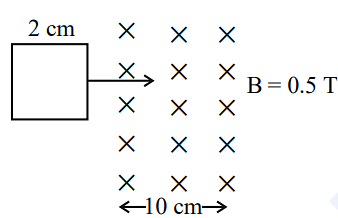
- KCET - 2023
- Physics
- Faradays laws of induction
- The current following through an inductance coil of self inductance 6 mH at different time instants is as shown. The emf induced between t = 20s and t = 40s is nearly
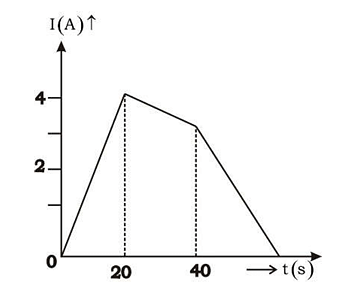
- KCET - 2021
- Physics
- Faradays laws of induction
View More Questions
Questions Asked in MGIMS Wardha exam
- What is the role of bithional in toilet soaps?
- MGIMS Wardha - 2015
- Chemistry in Everyday Life
- A drift velocity of free electrons in a conductor is $ {{\upsilon }_{d}} $ , when the current i is flowing in it. If both the radius and current are doubled, the drift velocity will be
- MGIMS Wardha - 2013
- Current electricity
- Mycoplasma is resistant for
- MGIMS Wardha - 2012
- Kingdom Monera
- A child swinging on a swing in sitting position, stands up, then the time period of swing will
- MGIMS Wardha - 2011
- Oscillations
- Mark the correct option. If a ball is projected with velocity $ {{v}_{o}} $ at an angle of elevation 30?, then
- MGIMS Wardha - 2011
- projectile motion
View More Questions
Concepts Used:
Faradays Laws of Induction
There are two laws, given by Faraday which explain the phenomena of electromagnetic induction:
Faraday's First Law:
Whenever a conductor is placed in a varying magnetic field, an emf is induced. If the conductor circuit is closed, a current is induced, known as the induced current.
Faraday's Second Law:
The Emf induced inside a coil is equal to the rate of change of associated magnetic flux.
This law can be mathematically written as:
∈\(-N {\triangle \phi \over \triangle t}\)
