A 1 m long wire is broken into two unequal parts X and Y. The X part of the wire is stretched into another wire W. Length of W is twice the length of X and the resistance of W is twice that of Y. Find the ratio of length of X and Y.
- 1:4
- 1:2
- 4:1
- 2:1
The Correct Option is B
Solution and Explanation
Rw = 2Ry
\(ρ\frac{2x}{\frac{A}{2}}=\frac{2ρ(1−x)}{A}\)
4x = 2(1 – x)
\(\frac{x}{1−x}=\frac{1}{2}\)
So, the correct option is (B): 1:2
Top Questions on Capacitors and Capacitance
- A parallel plate capacitor consisting of two circular plates of radius 10 cm is being charged by a constant current of 0.15 A. If the rate of change of potential difference between the plates is \( 7 \times 10^6 \, \text{V/s} \), then the integer value of the distance between the parallel plates is:
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
- A capacitor, \( C_1 = 6 \, \mu F \), is charged to a potential difference of \( V_1 = 5 \, \text{V} \) using a 5V battery. The battery is removed and another capacitor, \( C_2 = 12 \, \mu F \), is inserted in place of the battery. When the switch 'S' is closed, the charge flows between the capacitors for some time until equilibrium condition is reached. What are the charges \( q_1 \) and \( q_2 \) on the capacitors \( C_1 \) and \( C_2 \) when equilibrium condition is reached?
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
- A parallel plate capacitor of capacitance 1 μF is charged to a potential difference of 20 V. The distance between plates is 1 μm. The energy density between the plates of the capacitor is:
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
Identify the valid statements relevant to the given circuit at the instant when the key is closed.
\( \text{A} \): There will be no current through resistor R.
\( \text{B} \): There will be maximum current in the connecting wires.
\( \text{C} \): Potential difference between the capacitor plates A and B is minimum.
\( \text{D} \): Charge on the capacitor plates is minimum.
Choose the correct answer from the options given below:- JEE Main - 2025
- Physics
- Capacitors and Capacitance
- The position of a particle moving on x-axis is given by \( x(t) = A \sin t + B \cos^2 t + Ct^2 + D \), where \( t \) is time. The dimension of \( \frac{ABC}{D} \) is:
- JEE Main - 2025
- Physics
- Capacitors and Capacitance
Questions Asked in JEE Main exam
A conducting bar moves on two conducting rails as shown in the figure. A constant magnetic field \( B \) exists into the page. The bar starts to move from the vertex at time \( t = 0 \) with a constant velocity. If the induced EMF is \( E \propto t^n \), then the value of \( n \) is _____.
- JEE Main - 2025
- Magnetic Field
- Concentrated nitric acid is labelled as 75%by mass. The volume in mL of the solution which contains 30 g of nitric acid is: Given: Density of nitric acid solution is 1.25 g/mL.
- JEE Main - 2025
- Solutions
- A physical quantity \( Q \) is related to four observables \( a \), \( b \), \( c \), and \( d \) as follows: \[ Q = \frac{a b^4}{c d^2} \] Where:
- \( a = (60 \pm 3) \, \text{Pa} \),
- \( b = (20 \pm 0.1) \, \text{m} \),
- \( c = (40 \pm 0.2) \, \text{N·s/m}^2 \),
- \( d = (50 \pm 0.1) \, \text{m} \).
Then the percentage error in \( Q \) is:- JEE Main - 2025
- Error analysis
- Let circle $C$ be the image of
$$ x^2 + y^2 - 2x + 4y - 4 = 0 $$
in the line
$$ 2x - 3y + 5 = 0 $$
and $A$ be the point on $C$ such that $OA$ is parallel to the x-axis and $A$ lies on the right-hand side of the centre $O$ of $C$.
If $B(\alpha, \beta)$, with $\beta < 4$, lies on $C$ such that the length of the arc $AB$ is $\frac{1}{6}$ of the perimeter of $C$, then $\beta - \sqrt{3}\alpha$ is equal to: - Assume a living cell with 0.9%(\(w/w\)) of glucose solution (aqueous). This cell is immersed in another solution having equal mole fraction of glucose and water. (Consider the data up to first decimal place only) The cell will:
- JEE Main - 2025
- osmosis
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
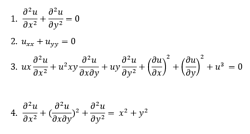
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
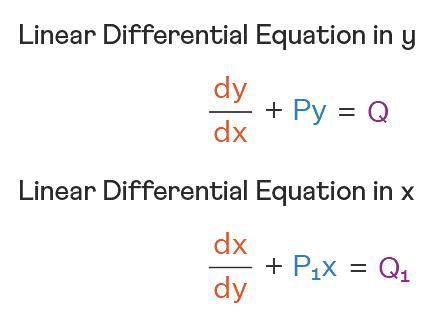
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations