Question

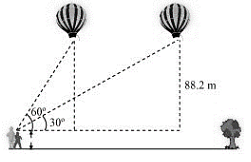
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.

Answer 1

Let the initial position A of balloon change to B after some time and CD be the girl.

In ∆ACE, 

\(\frac{AE}{ CE} = tan 60^{\degree}\)

\(\frac{AF - EF}{ CE} = tan 60^{\degree}\)

\(\frac{88.2 - 1.2}{ CE} = \sqrt3\)

\(\frac{87}{ CE} = \sqrt3\)

⇒ \(CE =\frac{ 87}{ \sqrt3} = 29\sqrt3 \,m\)

In ∆BCG, 

\(\frac{BG}{ CG}= tan 30^{\degree}\)

\(\frac{ 88.2 - 1.2}{ CG} = \frac{1}{ \sqrt3}\)

\(87 \sqrt3 m = \frac1{ CG}\)

Distance travelled by balloon = EG = CG − CE 
= \(( 87 \sqrt3 - 29 \sqrt3)\,m\)
= \(58 \sqrt3 \,m\)

Therefore, The distance travelled by balloon is \(58 \sqrt3 \,m\).