20 mL of 0.02 M K 2 Cr 2 O 7 solution is used for the titration of 10 mL of Fe 2+ solution in the acidic medium. The molarity of Fe 2+ solution is ______×10 –2 M. (Nearest integer)

Applying the law of equivalence, milliequivalents of Fe 2+ = milliequivalents of K 2 Cr 2 O 7 10 × 1 × M = 20 × 6 × .02 M = 24 × 10 –2 M &there4; Answer will be 24.

Question:

20 mL of 0.02 M K₂Cr₂O₇ solution is used for the titration of 10 mL of Fe²⁺ solution in the acidic medium. The molarity of Fe²⁺ solution is ______×10^–2 M. (Nearest integer)

Updated On: Sep 24, 2024

Hide Solution

Verified By Collegedunia

Correct Answer: 24

Solution and Explanation

Applying the law of equivalence,
milliequivalents of Fe²⁺= milliequivalents of K₂Cr₂O₇10 × 1 × M = 20 × 6 × .02
M = 24 × 10^–2 M
∴ Answer will be 24.

Was this answer helpful?

Questions Asked in JEE Main exam

View More Questions

Concepts Used:

Types of Differential Equations

There are various types of Differential Equation, such as:

Ordinary Differential Equations:

Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.

\(F(\frac{dy}{dt},y,t) = 0\)

Partial Differential Equations:

A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.

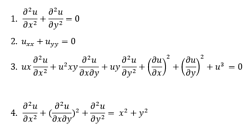
Linear Differential Equations:

It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.

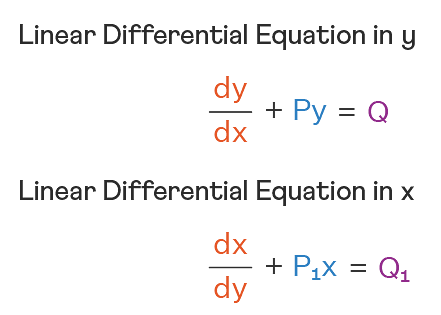
Homogeneous Differential Equations:

When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.

\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)

Read More: Differential Equations

20 mL of 0.02 M K2Cr2O7 solution is used for the titration of 10 mL of Fe2+ solution in the acidic medium. The molarity of Fe2+ solution is ______×10–2 M. (Nearest integer)