Question:
Which of the following is true?
Which of the following is true?
Updated On: Jun 1, 2024
- Φ = 0
- n(Φ) = 0
- Φ = {0}
- n(Φ') = 0
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
The correct option is (B): n(Φ) = 0.
Was this answer helpful?
0
0
Top Questions on Sets
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
- Let $S_1 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≥ x^2, x, y ≥ 0}$ and $S_2 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≤ x^2, x, y ≥ 0}.$ Then, which of the following is CORRECT ?
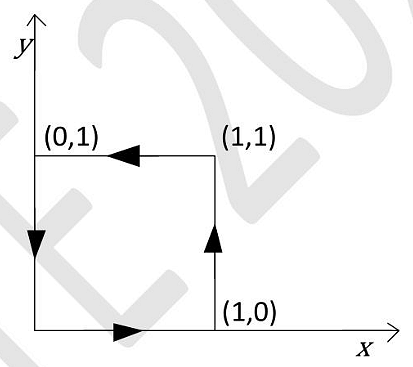
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
- If \(A=\begin{pmatrix} 1 & -1 \\ 2 & -2 \end{pmatrix}\), the eigenvalues of A are _____
View More Questions
Questions Asked in TS POLYCET exam
- A tangent AB at a point 'A' of a circle of radius 7 cm meets a line through the centre 'C' at a point 'B' so that CB=11 cm, then the length of AB =
- TS POLYCET - 2023
- Tangent to a Circle
- \(\triangle ABC \sim \triangle DEF\) and their areas are respectively \(81 \text{ cm}^2 \quad \text{and} \quad 225 \text{ cm}^2\); if \(EF = 5 cm\), then \(BC=\)
- TS POLYCET - 2023
- Triangles
- If \(\sec \theta = \frac{2}{\sqrt{3}}\),then \(cosθ=\)
- TS POLYCET - 2023
- Trigonometry
- The value of \(\tan 26^\circ. \tan 64^\circ\) is
- TS POLYCET - 2023
- Trigonometry
- In the figure, if AP and AQ are the two tangents to a circle with centre 'O' so that \(∠OQP=15°\), then \(∠QAP=\)
- TS POLYCET - 2023
- Tangent to a Circle
View More Questions