Question:
If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
Updated On: May 7, 2024
- {3,4} ∈ A
- {{3,4}}⊂A
- {3,4}⊂A
- None of these
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct option is (C): {3,4}⊂A.
Was this answer helpful?
0
0
Top Questions on Sets
- Let $S_1 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≥ x^2, x, y ≥ 0}$ and $S_2 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≤ x^2, x, y ≥ 0}.$ Then, which of the following is CORRECT ?
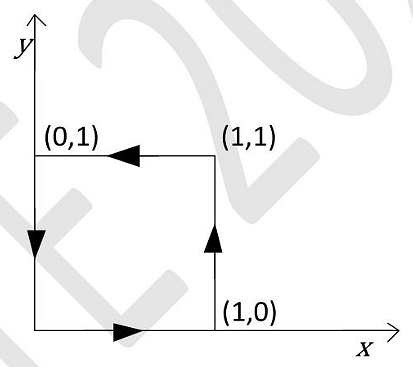
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
- If \(A=\begin{pmatrix} 1 & -1 \\ 2 & -2 \end{pmatrix}\), the eigenvalues of A are _____
- If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
- Given the following sets:
𝐴 = {2, 4, 6, 8, 10, 12}
𝐵 = {8, 10, 12, 14, 16, 18}
𝐶 = {7, 8, 9, 10 11, 12, 13}
(𝐴 ∩ 𝐵) ∪ (𝐵 ∩ 𝐶) is
View More Questions
Questions Asked in AP POLYCET exam
- If the centroid of a triangle formed by the points \((a,b), (b, c)\) and \((c,a)\) is at the origin, then \(a^3+b^3+c^3 =\)
- AP POLYCET - 2024
- Triangles
- If a sin 45°= b cosec 30°, then the value of \(\frac {a^4}{b^4}\) is
- AP POLYCET - 2024
- Trigonometry
- The ratio of the sum and product of the roots of the quadratic equation \(7x^2-12x+18=0\) is
- AP POLYCET - 2024
- Quadratic Equations
- If the slope of the line joining the points (4,2) and (3,-k) is -2, then the value of k is
- AP POLYCET - 2024
- Slope of a line
- If 25 cm each is the object and image distances due to convex lens, then its focal length is
- AP POLYCET - 2024
- Light - Reflection and Refraction
View More Questions