If A and B are the two sets containing 3 and 6 elements respectively, then what can be the maximum number of elements in A∪B?
- 9
- 10
- 11
- 12
The Correct Option is A
Solution and Explanation
Let A and B be two sets with |A| = 3 and |B| = 6.
The number of elements in the union of A and B is given by the principle of inclusion-exclusion: |A U B| = |A| + |B| - |A ∩ B|.
The maximum number of elements in A U B occurs when the intersection of A and B is minimal.
Case 1: A and B are disjoint sets, i.e., A ∩ B = ∅. In this case, |A ∩ B| = 0. |A U B| = |A| + |B| = 3 + 6 = 9
Case 2: A is a subset of B, i.e., A ⊆ B. In this case, A ∩ B = A, so |A ∩ B| = |A| = 3. |A U B| = |A| + |B| - |A ∩ B| = 3 + 6 - 3 = 6
Case 3: A and B have some elements in common. Let |A ∩ B| = k.
Since A ∩ B ⊆ A, we have 0 ≤ k ≤ |A| = 3. Since A ∩ B ⊆ B, we have 0 ≤ k ≤ |B| = 6. Thus, 0 ≤ k ≤ 3. |A U B| = |A| + |B| - |A ∩ B| = 3 + 6 - k = 9 - k.
To maximize |A U B|, we need to minimize k.
The minimum value of k is 0. |A U B| = 9 - 0 = 9.
Therefore, the maximum number of elements in A U B is 9.
Top Questions on Sets
- Mode of the data \( 19, 2, 6, 12, 12, 3, 5, 6, 18, 14, 6, 17, 2 \) is:
- The mean and mode of 5, 3, 9, 1, 9, 8, 9, 4 are m and n respectively, the value of m+n is?
- If A = {1, 2, {3, 4}, 5}, then which of the following is incorrect?
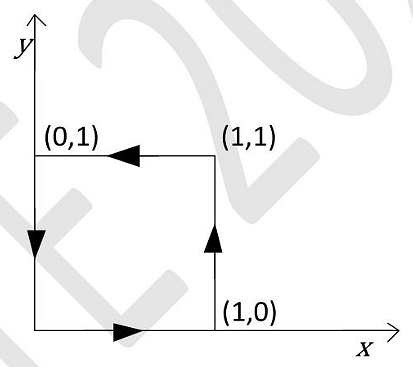
- For \(\vec{F}=(x+y)\hat{i}+(x+y)\hat{j}\) the value of \(\oint\vec{F}.d\vec{r}\) along the path shown in the figure is ________. Give your answer as an integer.
- Let $S_1 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≥ x^2, x, y ≥ 0}$ and $S_2 = {(x, y) ∈ R^2 ∶ x + y ≥ 1, x + y ≤ 2, y ≤ x^2, x, y ≥ 0}.$ Then, which of the following is CORRECT ?
Questions Asked in AP POLYCET exam
- The magnetic field produced by a current carrying circular loop is strongest at
- AP POLYCET - 2025
- Magnetic Field
- The region surrounding a magnet in which the influence of that magnet can be detected is called
- AP POLYCET - 2025
- Magnetic Field
- If the electric current through a copper wire increases, the magnitude of the magnetic field produced at a given point:
- AP POLYCET - 2025
- Magnetic Field
- The magnetic field at all points inside a solenoid carrying electric current:
- AP POLYCET - 2025
- Magnetic Field
- Ram and Syam are friends. Probability that both will have same birthday is:
- AP POLYCET - 2025
- Probability