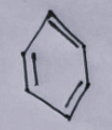
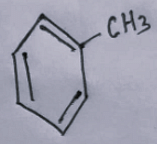
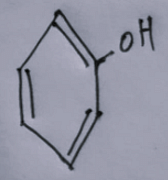
Which is following compound is easily attacked by electrophile?
The Correct Option is D
Solution and Explanation
Top Questions on Organic Chemistry - Some Basic Principles and Techniques
- An isomer of C$_8$H$_{18}$ is X. This has five primary, one tertiary and one quaternary carbon. What is X?
- TS EAMCET - 2025
- Chemistry
- Organic Chemistry - Some Basic Principles and Techniques
- What are X and Y in the following reaction sequence?
2-Methylbutane $\xrightarrow{\text{KMnO}_4}$ X$\xrightarrow{\text{Y}}$ C5H11Cl- TS EAMCET - 2025
- Chemistry
- Organic Chemistry - Some Basic Principles and Techniques
- X and Y in reaction sequence:
- TS EAMCET - 2025
- Chemistry
- Organic Chemistry - Some Basic Principles and Techniques
- IUPAC names of benzene derivatives are respectively:
- TS EAMCET - 2025
- Chemistry
- Organic Chemistry - Some Basic Principles and Techniques
- The IUPAC name of the following compound is
- TS EAMCET - 2025
- Chemistry
- Organic Chemistry - Some Basic Principles and Techniques
Questions Asked in JEE Main exam
- The number of non-empty equivalence relations on the set \(\{1,2,3\}\) is :
- JEE Main - 2025
- Set Theory
- Let \( [x] \) denote the greatest integer function, and let \( m \) and \( n \) respectively be the numbers of the points, where the function \( f(x) = [x] + |x - 2| \), \( -2<x<3 \), is not continuous and not differentiable. Then \( m + n \) is equal to:
- JEE Main - 2025
- Differential Equations
- Two charges \( 7 \, \mu C \) and \( -4 \, \mu C \) are placed at \( (-7 \, \text{cm}, 0, 0) \) and \( (7 \, \text{cm}, 0, 0) \) respectively. Given, \( \epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2 \text{N}^{-1} \text{m}^{-2} \), the electrostatic potential energy of the charge configuration is:
- JEE Main - 2025
- Electrostatics and Potential Energy
Let \( y^2 = 12x \) be the parabola and \( S \) its focus. Let \( PQ \) be a focal chord of the parabola such that \( (SP)(SQ) = \frac{147}{4} \). Let \( C \) be the circle described by taking \( PQ \) as a diameter. If the equation of the circle \( C \) is: \[ 64x^2 + 64y^2 - \alpha x - 64\sqrt{3}y = \beta, \] then \( \beta - \alpha \) is equal to:
- JEE Main - 2025
- Parabola
Let one focus of the hyperbola $ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $ be at $ (\sqrt{10}, 0) $, and the corresponding directrix be $ x = \frac{\sqrt{10}}{2} $. If $ e $ and $ l $ are the eccentricity and the latus rectum respectively, then $ 9(e^2 + l) $ is equal to:
- JEE Main - 2025
- Conic sections
Concepts Used:
Organic Chemistry - Some Basic Principles and Techniques
Organic Chemistry is a subset of chemistry dealing with compounds of carbon. Therefore, we can say that Organic chemistry is the chemistry of carbon compounds and is 200-225 years old. Carbon forms bond with itself to form long chains of hydrocarbons, e.g.CH4, methane and CH3-CH3 ethane. Carbon has the ability to form carbon-carbon bonds quite elaborately. Polymers like polyethylene is a linear chain where hundreds of CH2 are linked together.
Read Also: Organic Compounds
Importance of Organic Chemistry:
Organic chemistry is applicable in a variety of areas including-
- Medicines: Example- Aspirin which is a headache medicine and Ibuprofen is a painkiller, both are organic compounds. Other examples include paracetamol.
- Food: Example- Starch which is a carbohydrate is an organic compound and a constituent of rice and other grains. It is the source of energy.
- Clothing: Example- Nylon, Polyester and Cotton are forms of organic compounds.
- Fuels: Examples- Gasoline, Petrol and Diesel are organic compounds used in the automobile industry at large.