Two thin biconvex lenses have focal lengths $f _{1}$ and $f _{2} .$ A third thin biconcave lens has focal length of $f_{3} .$ If the two biconvex lenses are in contact, the total power of the lenses is $P _{1}$. If the first convex lens is in contact with the third lens, the total power is $P _{2}$. If the second lens is in contact with the third lens, the total power is $P _{3}$ then
- $P _{1}=\frac{ f _{1} f _{2}}{ f _{1}- f _{2}}, P _{2}=\frac{ f _{1} f _{3}}{ f _{3}- f _{1}}$ and $P _{3}=\frac{ f _{2} f _{3}}{ f _{3}- f _{2}}$
- $P _{1}=\frac{ f _{1}- f _{2}}{ f _{1} f _{2}}, P _{2}=\frac{ f _{3}- f _{1}}{ f _{3}+ f _{1}}$ and $P _{3}=\frac{ f _{3}- f _{2}}{ f _{2} f _{3}}$
- $P _{1}=\frac{ f _{1}- f _{2}}{ f _{1} f _{2}}, P _{2}=\frac{ f _{3}- f _{1}}{ f _{1} f _{3}}$ and $P _{3}=\frac{ f _{3}- f _{2}}{ f _{2} f _{3}}$
- $P_{1}=\frac{f_{1}+f_{2}}{f_{1} f_{2}}, P_{2}=\frac{f_{3}-f_{1}}{f_{1} f_{3}}$ and $P_{3}=\frac{f_{3}-f_{2}}{f_{2} f_{3}}$
The Correct Option is D
Approach Solution - 1
To determine the total power of lenses in contact, we use the fundamental formula for lens power:
\(P = \frac{1}{f}\)
Where \(P\) is the power and \(f\) is the focal length of the lens.
When multiple lenses are in contact, their combined power is the sum of their individual powers:
\(P_{total} = P_1 + P_2 + P_3 + \ldots\)
- Analyzing the given situation:
- For the combination of two biconvex lenses with focal lengths \(f_1\) and \(f_2\), the total power is given by:
\(P_1 = \frac{1}{f_1} + \frac{1}{f_2} = \frac{f_1 + f_2}{f_1 f_2}\)
- For the combination of the first biconvex and the biconcave lens with focal lengths \(f_1\) and \(f_3\) respectively, the total power is:
\(P_2 = \frac{1}{f_1} + \frac{1}{-f_3} = \frac{f_3 - f_1}{f_1 f_3}\)
- For the combination of the second biconvex and the biconcave lens with focal lengths \(f_2\) and \(f_3\) respectively, the total power is:
\(P_3 = \frac{1}{f_2} + \frac{1}{-f_3} = \frac{f_3 - f_2}{f_2 f_3}\)
- Justifying the Correct Option:
- The derived expressions for the total powers \(P_1\), \(P_2\), and \(P_3\) match the given correct answer option:
- \(P_1 = \frac{f_1 + f_2}{f_1 f_2}\)
- \(P_2 = \frac{f_3 - f_1}{f_1 f_3}\)
- \(P_3 = \frac{f_3 - f_2}{f_2 f_3}\)
Conclusion: Thus, based on the above analysis and calculations, the correct answer is \(P_{1}=\frac{f_{1}+f_{2}}{f_{1} f_{2}}, P_{2}=\frac{f_{3}-f_{1}}{f_{1} f_{3}}\) and \(P_{3}=\frac{f_{3}-f_{2}}{f_{2} f_{3}}\).
Approach Solution -2
$f _{2}=+ f _{2}$
$f _{3}=- f _{3}$
$\frac{1}{F_{R}}=\frac{1}{f_{1}}+\frac{1}{f_{2}}$
$P_{R}=\frac{1}{f_{1}}+\frac{1}{f_{2}}$
$P_{1}=\frac{1}{f_{1}}+\frac{1}{f_{2}}=\frac{f_{2}+f_{1}}{f_{1} f_{2}}$
$P_{2}=\frac{1}{f_{1}}+\frac{1}{f_{3}}=\frac{f_{3}-f_{1}}{f_{1} f_{3}}$
$P_{2}=\frac{1}{f_{2}}+\frac{1}{f_{3}}=\frac{f_{3}-f_{2}}{f_{2} f_{3}}$
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in KCET exam
Match the following:
In the following, \( [x] \) denotes the greatest integer less than or equal to \( x \).
Choose the correct answer from the options given below:- KCET - 2025
- Differentiability
- If \[ y = \frac{\cos x}{1 + \sin x} \] then:
- KCET - 2025
- Differentiability
- A function \( f(x) \) is given by:
\[ f(x) = \begin{cases} \frac{1}{e^x - 1}, & \text{if } x \neq 0 \\ \frac{1}{e^x + 1}, & \text{if } x = 0 \end{cases} \] Then, which of the following is true?- KCET - 2025
- Limits
- The function f(x) is given by:
For x < 0:
f(x) = ex + axFor x ≥ 0:
f(x) = b(x - 1)2
The function is differentiable at x = 0. Then,- KCET - 2025
- Differentiability
- The function \( f(x) = \tan x - x \)
- KCET - 2025
- Derivatives
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
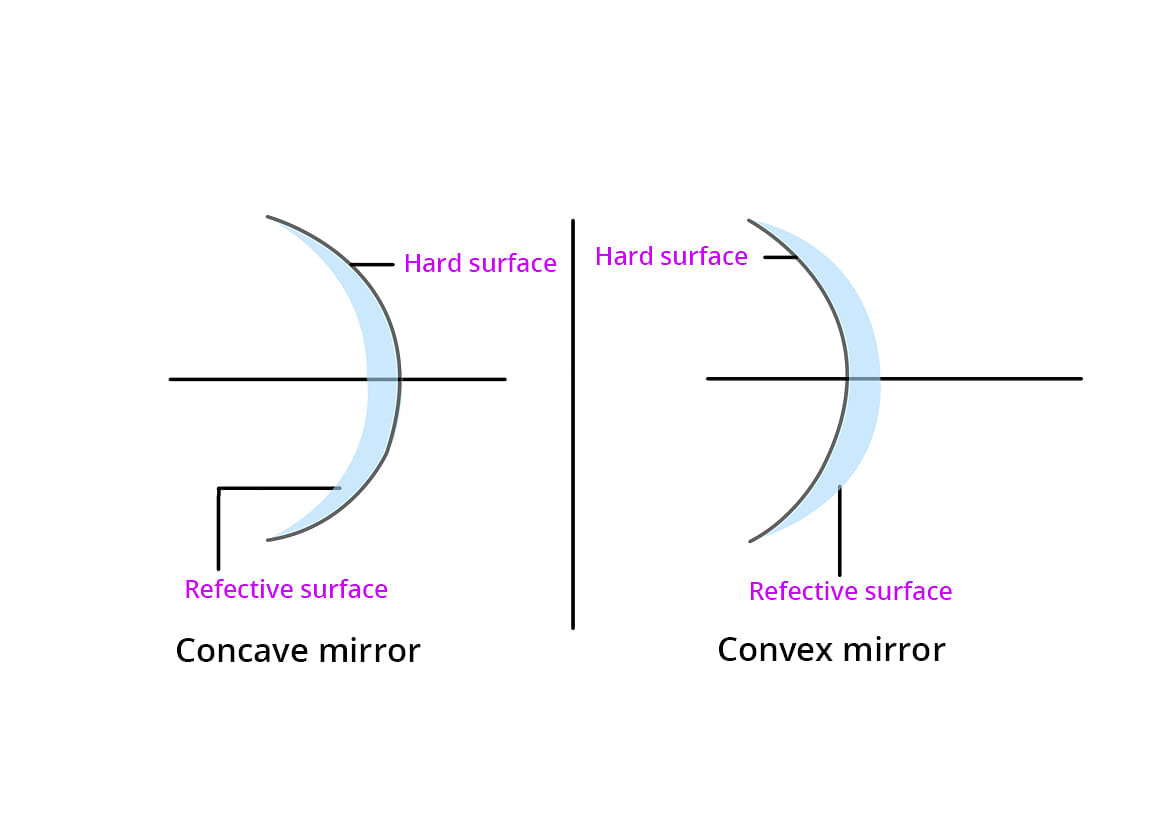
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.