Question:
The wavelength of characteristic K\(_\alpha\) X-ray photons from Mo (atomic number 42) is ............. Å. (Round off to one decimal place).
The wavelength of characteristic K\(_\alpha\) X-ray photons from Mo (atomic number 42) is ............. Å. (Round off to one decimal place).
Show Hint
The characteristic X-ray wavelengths can be calculated using the Rydberg formula, where \( Z \) is the atomic number, and \( n_1 \) and \( n_2 \) are the principal quantum numbers of the initial and final energy levels.
Updated On: Dec 6, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 0.6
Solution and Explanation
Step 1: Use the Rydberg formula for X-ray wavelengths.
The characteristic K\(_\alpha\) X-ray wavelength for an atom can be calculated using the formula: \[ \lambda = \frac{R \cdot Z^2}{n_1^2 - n_2^2}, \] where \[ R = 1.097 \times 10^7 \, \text{m}^{-1} \quad \text{(Rydberg constant)} \quad \text{and} \quad Z = 42 \quad \text{(atomic number of Mo)}. \] For the K\(_\alpha\) transition, \( n_1 = 2 \) and \( n_2 = 1 \), so \[ \lambda = \frac{1.097 \times 10^7 \times 42^2}{2^2 - 1^2}. \] Step 2: Simplify and calculate the wavelength.
First, calculate the numerator: \[ 42^2 = 1764, \quad 1.097 \times 10^7 \times 1764 = 1.938 \times 10^{10}. \] Now, calculate the denominator: \[ 2^2 - 1^2 = 4 - 1 = 3. \] Thus, \[ \lambda = \frac{1.938 \times 10^{10}}{3} = 6.46 \times 10^9 \, \text{m}. \] Converting to nanometers: \[ \lambda = 6.46 \, \text{nm} = 0.646 \, \text{Å}. \] Final Answer: The wavelength of K\(_\alpha\) X-ray photons from Mo is \( \boxed{0.6} \, \text{Å}. \)
The characteristic K\(_\alpha\) X-ray wavelength for an atom can be calculated using the formula: \[ \lambda = \frac{R \cdot Z^2}{n_1^2 - n_2^2}, \] where \[ R = 1.097 \times 10^7 \, \text{m}^{-1} \quad \text{(Rydberg constant)} \quad \text{and} \quad Z = 42 \quad \text{(atomic number of Mo)}. \] For the K\(_\alpha\) transition, \( n_1 = 2 \) and \( n_2 = 1 \), so \[ \lambda = \frac{1.097 \times 10^7 \times 42^2}{2^2 - 1^2}. \] Step 2: Simplify and calculate the wavelength.
First, calculate the numerator: \[ 42^2 = 1764, \quad 1.097 \times 10^7 \times 1764 = 1.938 \times 10^{10}. \] Now, calculate the denominator: \[ 2^2 - 1^2 = 4 - 1 = 3. \] Thus, \[ \lambda = \frac{1.938 \times 10^{10}}{3} = 6.46 \times 10^9 \, \text{m}. \] Converting to nanometers: \[ \lambda = 6.46 \, \text{nm} = 0.646 \, \text{Å}. \] Final Answer: The wavelength of K\(_\alpha\) X-ray photons from Mo is \( \boxed{0.6} \, \text{Å}. \)
Was this answer helpful?
0
0
Top Questions on X Rays and the Ordering of the Elements
- The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The minimum wavelength of X-rays produced by 20 keV electrons is nearly
- AP EAPCET - 2025
- Physics
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
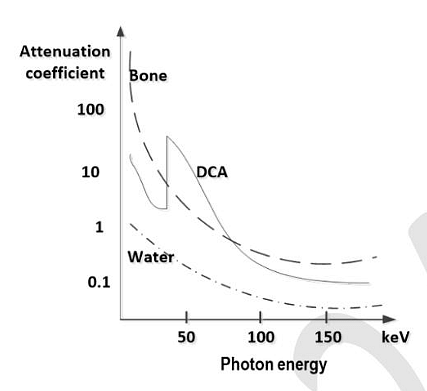
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
View More Questions
Questions Asked in IIT JAM exam
- Consider a volume V enclosed by a closed surface S having unit surface normal \(\hat{n}\). For \(\mathbf{r} = x\hat{i} + y\hat{j} + z\hat{k}\), the value of the surface integral \(\frac{1}{9} \oint_{S} \mathbf{r} \cdot \hat{n} \,dS\) is
- IIT JAM PH - 2025
- Vector Calculus
- For a Zener diode as shown in the circuit diagram below, the Zener voltage \(V_Z\) is 3.7 V. For a load resistance (\(R_L\)) of 1 k\(\Omega\), a current \(I_1\) flows through the load. If \(R_L\) is decreased to 500 \(\Omega\), the current changes to \(I_2\). The ratio \(\frac{I_2}{I_1}\) is \rule{1cm{0.15mm}. (up to two decimal places)}

- IIT JAM PH - 2025
- Analog Electronics
- The shortest distance between an object and its real image formed by a thin convex lens of focal length 20 cm is _____ cm. (in integer)
- If \(\left(\frac{1-i}{1+i}\right)^{n/2} = -1\), where \(i = \sqrt{-1}\), one possible value of n is
- IIT JAM PH - 2025
- Complex numbers
- In a two-level atomic system, the excited state is 0.2 eV above the ground state. Considering the Maxwell-Boltzmann distribution, the temperature at which 2% of the atoms will be in the excited state is _____ K. (up to two decimal places)
(Boltzmann constant \(k_B = 8.62 \times 10^{-5}\) eV/K)
- IIT JAM PH - 2025
- Mechanics
View More Questions