Question:
The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
Show Hint
The formula \( \lambda_{\text{min}} (\text{Å}) \approx \frac{12400}{V (\text{volts})} \) is extremely useful and a major time-saver in exams. Memorize it. The constant 12400 comes from the product \(hc/e\) in units of eV·Å.
Updated On: Jan 17, 2026
- 25 Å
- 2.5 Å
- 0.25 Å
- 0.025 Å
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Step 1: Understanding the Concept:
When electrons are accelerated through a potential difference V and strike a target, they produce a continuous spectrum of X-rays (bremsstrahlung radiation). The shortest possible wavelength (\(\lambda_{\text{min}}\)) is produced when an electron loses all its kinetic energy in a single interaction, creating a single X-ray photon of maximum energy. This is described by the Duane-Hunt law.
Step 2: Key Formula or Approach:
The kinetic energy of an electron accelerated through a potential V is \( E = eV \).
The energy of a photon is \( E = hf = \frac{hc}{\lambda} \).
For the shortest wavelength, the entire kinetic energy of the electron is converted into the energy of one photon:
\[ eV = \frac{hc}{\lambda_{\text{min}}} \]
\[ \lambda_{\text{min}} = \frac{hc}{eV} \]
A very useful shortcut for this calculation is:
\[ \lambda_{\text{min}} (\text{in Å}) \approx \frac{12400}{V (\text{in volts})} \]
Step 3: Detailed Explanation:
Given the accelerating potential \( V = 50 \) kV \( = 50 \times 10^3 \) V \( = 50000 \) V.
Using the shortcut formula:
\[ \lambda_{\text{min}} (\text{Å}) = \frac{12400}{50000} \]
\[ \lambda_{\text{min}} (\text{Å}) = \frac{124}{500} = 0.248 \text{ Å} \]
Step 4: Final Answer:
The calculated value of 0.248 Å is closest to the option 0.25 Å.
When electrons are accelerated through a potential difference V and strike a target, they produce a continuous spectrum of X-rays (bremsstrahlung radiation). The shortest possible wavelength (\(\lambda_{\text{min}}\)) is produced when an electron loses all its kinetic energy in a single interaction, creating a single X-ray photon of maximum energy. This is described by the Duane-Hunt law.
Step 2: Key Formula or Approach:
The kinetic energy of an electron accelerated through a potential V is \( E = eV \).
The energy of a photon is \( E = hf = \frac{hc}{\lambda} \).
For the shortest wavelength, the entire kinetic energy of the electron is converted into the energy of one photon:
\[ eV = \frac{hc}{\lambda_{\text{min}}} \]
\[ \lambda_{\text{min}} = \frac{hc}{eV} \]
A very useful shortcut for this calculation is:
\[ \lambda_{\text{min}} (\text{in Å}) \approx \frac{12400}{V (\text{in volts})} \]
Step 3: Detailed Explanation:
Given the accelerating potential \( V = 50 \) kV \( = 50 \times 10^3 \) V \( = 50000 \) V.
Using the shortcut formula:
\[ \lambda_{\text{min}} (\text{Å}) = \frac{12400}{50000} \]
\[ \lambda_{\text{min}} (\text{Å}) = \frac{124}{500} = 0.248 \text{ Å} \]
Step 4: Final Answer:
The calculated value of 0.248 Å is closest to the option 0.25 Å.
Was this answer helpful?
0
0
Top Questions on X Rays and the Ordering of the Elements
- In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The minimum wavelength of X-rays produced by 20 keV electrons is nearly
- AP EAPCET - 2025
- Physics
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
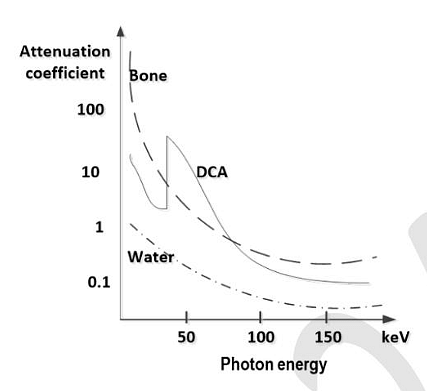
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- Which one of the following events is NOT typically encountered in diagnostic X-ray projection radiography ?
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
View More Questions
Questions Asked in CUET PG exam
- According to Erikson's stages of Psychosocial Development, the "trust versus mistrust phase" is the developmental task of:
- CUET (PG) - 2025
- Developmental Psychology
- Fill in the blank with the appropriate word from the options given below: He, as well as his friends, ............ denied entry to the stadium.
- CUET (PG) - 2025
- Subject Verb Agreement
- Who first used the term 'Negative Capability'?
- CUET (PG) - 2025
- Literary Theory
- If \( \frac{1}{9!} + \frac{1}{10!} = \frac{x}{11!} \), then the value of \( x \) is:
- CUET (PG) - 2025
- Factorial Equations
- The genetic constitution of the combined paternal and maternal DNA responsible for producing the different ABO blood groups is referred as:
- CUET (PG) - 2025
- Forensic Biology
View More Questions