Question:
In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
In Laue's technique of X-ray diffraction, a single crystal is held stationary and the beam of white radiation of wavelength \(\lambda\) is inclined at which condition with glancing angle (\(\theta\)):
Show Hint
Memorize the key features of the three main XRD methods:
\textbf{Laue Method:} Stationary single crystal, variable \(\lambda\) (white X-rays). Used for crystal orientation.
\textbf{Rotating Crystal Method:} Rotating single crystal (variable \(\theta\)), fixed \(\lambda\) (monochromatic X-rays). Used for determining lattice parameters.
\textbf{Powder Method:} Powdered sample (all \(\theta\) orientations available), fixed \(\lambda\). Used for identifying crystal structure and phase analysis.
\textbf{Laue Method:} Stationary single crystal, variable \(\lambda\) (white X-rays). Used for crystal orientation.
\textbf{Rotating Crystal Method:} Rotating single crystal (variable \(\theta\)), fixed \(\lambda\) (monochromatic X-rays). Used for determining lattice parameters.
\textbf{Powder Method:} Powdered sample (all \(\theta\) orientations available), fixed \(\lambda\). Used for identifying crystal structure and phase analysis.
Updated On: Jan 17, 2026
- \(\theta\) is fixed while \(\lambda\) varies
- \(\lambda\) is fixed while \(\theta\) varies
- \(\lambda\) is fixed while both \(\theta\) and distance varies
- \(\theta\) is fixed while both \(\lambda\) and distance varies
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Step 1: Understanding the Concept:
The question asks about the experimental conditions of the Laue method, one of the primary techniques for X-ray diffraction. We need to identify which parameters in Bragg's law (\(2d\sin\theta = n\lambda\)) are fixed and which are variable in this method.
Step 2: Detailed Explanation:
In the Laue diffraction technique:
1. A single crystal is used.
2. The crystal is held stationary, meaning its orientation with respect to the incoming X-ray beam is fixed. For any given set of crystal planes (with interplanar spacing 'd'), the glancing angle \(\theta\) is therefore also fixed.
3. The crystal is irradiated with white radiation, which is a continuous spectrum of X-rays containing a range of wavelengths. This means the wavelength \(\lambda\) is variable.
Bragg's law is satisfied when, for a set of planes with fixed \(d\) and \(\theta\), the beam contains a wavelength \(\lambda\) that fulfills the equation \( \lambda = (2d/n)\sin\theta \). Since the incident beam has a continuous spectrum of \(\lambda\), some wavelengths will always satisfy the condition for various planes, producing a diffraction pattern of spots.
Step 3: Final Answer:
In the Laue technique, the angle \(\theta\) is fixed for any given plane, and the wavelength \(\lambda\) is varied.
The question asks about the experimental conditions of the Laue method, one of the primary techniques for X-ray diffraction. We need to identify which parameters in Bragg's law (\(2d\sin\theta = n\lambda\)) are fixed and which are variable in this method.
Step 2: Detailed Explanation:
In the Laue diffraction technique:
1. A single crystal is used.
2. The crystal is held stationary, meaning its orientation with respect to the incoming X-ray beam is fixed. For any given set of crystal planes (with interplanar spacing 'd'), the glancing angle \(\theta\) is therefore also fixed.
3. The crystal is irradiated with white radiation, which is a continuous spectrum of X-rays containing a range of wavelengths. This means the wavelength \(\lambda\) is variable.
Bragg's law is satisfied when, for a set of planes with fixed \(d\) and \(\theta\), the beam contains a wavelength \(\lambda\) that fulfills the equation \( \lambda = (2d/n)\sin\theta \). Since the incident beam has a continuous spectrum of \(\lambda\), some wavelengths will always satisfy the condition for various planes, producing a diffraction pattern of spots.
Step 3: Final Answer:
In the Laue technique, the angle \(\theta\) is fixed for any given plane, and the wavelength \(\lambda\) is varied.
Was this answer helpful?
0
0
Top Questions on X Rays and the Ordering of the Elements
- The shortest wavelength, present in X-rays produced by an accelerating potential of 50kV, is:
- CUET (PG) - 2025
- Material Science and Technology
- X Rays and the Ordering of the Elements
- The minimum wavelength of X-rays produced by 20 keV electrons is nearly
- AP EAPCET - 2025
- Physics
- X Rays and the Ordering of the Elements
- An X-ray beam of initial intensity I0 of 70 keV imaging the chest is assumed to undergo attenuation through the muscle tissue for a thickness of 16 cm and further through the bone tissue for a thickness of 4 cm. The half value layer (HVL) thicknesses for the muscle and bone are 3.5 cm and 1.8 cm, respectively. The percentage of X-ray intensity transmitted through the body is ________.
Give your answer rounded off to 2 decimal places.- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- The X-ray attenuation coefficients as a function of photon energy for three materials are shown in the figure below. A tissue phantom containing these three materials is imaged at two different X-ray photon energies of 50 keV and 150 keV. When the developed X-ray film is viewed, which of the following statements is/are TRUE ?
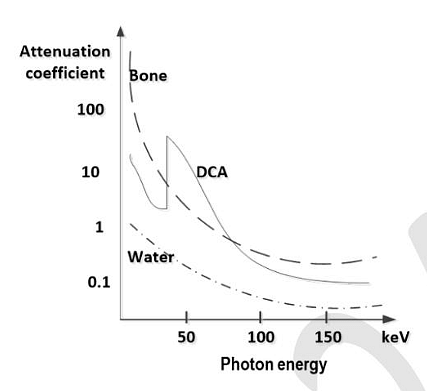
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
- Which one of the following events is NOT typically encountered in diagnostic X-ray projection radiography ?
- GATE BM - 2024
- Medical Imaging Systems
- X Rays and the Ordering of the Elements
View More Questions
Questions Asked in CUET PG exam
- According to Erikson's stages of Psychosocial Development, the "trust versus mistrust phase" is the developmental task of:
- CUET (PG) - 2025
- Developmental Psychology
- Fill in the blank with the appropriate word from the options given below: He, as well as his friends, ............ denied entry to the stadium.
- CUET (PG) - 2025
- Subject Verb Agreement
- Who first used the term 'Negative Capability'?
- CUET (PG) - 2025
- Literary Theory
- If \( \frac{1}{9!} + \frac{1}{10!} = \frac{x}{11!} \), then the value of \( x \) is:
- CUET (PG) - 2025
- Factorial Equations
- The genetic constitution of the combined paternal and maternal DNA responsible for producing the different ABO blood groups is referred as:
- CUET (PG) - 2025
- Forensic Biology
View More Questions