Question:
The variation of stopping potential (V0) as a function of the frequency (v) of the incident light for a metal is shown in figure. The work function of the surface is
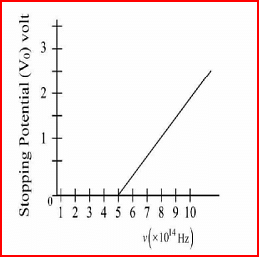
The variation of stopping potential (V0) as a function of the frequency (v) of the incident light for a metal is shown in figure. The work function of the surface is


Updated On: Mar 21, 2025
- 1.36 eV
- 2.98 eV
- 2.07 eV
- 18.6 eV
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Step 1: Understanding the photoelectric equation.
In the photoelectric effect, the stopping potential (\( V_0 \)) is related to the frequency (\( v \)) of the incident light by the equation: \[ eV_0 = h(v - v_{\text{th}}) \] Where:
\( V_0 \) is the stopping potential (in volts).
\( v \) is the frequency of the incident light (in Hz).
\( v_{\text{th}} \) is the threshold frequency (below which no photoelectric emission occurs).
\( e \) is the charge of the electron (\( 1.6 \times 10^{-19} \, \text{C} \)).
\( h \) is Planck's constant (\( 6.6 \times 10^{-34} \, \text{J} \cdot \text{s} \)).
Step 2: Identifying the threshold frequency.
From the graph, we can observe that the stopping potential becomes non-zero at a frequency of approximately \( 5 \times 10^{14} \, \text{Hz} \). This is the threshold frequency \( v_{\text{th}} \).
Step 3: Calculating the work function.
At the threshold frequency, the stopping potential is zero. We use the equation: \[ \phi = h v_{\text{th}} \] Substituting the values: \[ \phi = (6.6 \times 10^{-34}) \times (5 \times 10^{14}) = 33 \times 10^{-20} \, \text{J} \] \[ \phi = 3.3 \times 10^{-19} \, \text{J} \] To convert this to eV, divide by the charge of the electron: \[ \phi = \frac{3.3 \times 10^{-19}}{1.6 \times 10^{-19}} \, \text{eV} = 2.07 \, \text{eV} \] Thus, the work function is \( \phi = 2.07 \, \text{eV} \).
In the photoelectric effect, the stopping potential (\( V_0 \)) is related to the frequency (\( v \)) of the incident light by the equation: \[ eV_0 = h(v - v_{\text{th}}) \] Where:
\( V_0 \) is the stopping potential (in volts).
\( v \) is the frequency of the incident light (in Hz).
\( v_{\text{th}} \) is the threshold frequency (below which no photoelectric emission occurs).
\( e \) is the charge of the electron (\( 1.6 \times 10^{-19} \, \text{C} \)).
\( h \) is Planck's constant (\( 6.6 \times 10^{-34} \, \text{J} \cdot \text{s} \)).
Step 2: Identifying the threshold frequency.
From the graph, we can observe that the stopping potential becomes non-zero at a frequency of approximately \( 5 \times 10^{14} \, \text{Hz} \). This is the threshold frequency \( v_{\text{th}} \).
Step 3: Calculating the work function.
At the threshold frequency, the stopping potential is zero. We use the equation: \[ \phi = h v_{\text{th}} \] Substituting the values: \[ \phi = (6.6 \times 10^{-34}) \times (5 \times 10^{14}) = 33 \times 10^{-20} \, \text{J} \] \[ \phi = 3.3 \times 10^{-19} \, \text{J} \] To convert this to eV, divide by the charge of the electron: \[ \phi = \frac{3.3 \times 10^{-19}}{1.6 \times 10^{-19}} \, \text{eV} = 2.07 \, \text{eV} \] Thus, the work function is \( \phi = 2.07 \, \text{eV} \).
Was this answer helpful?
0
1
Top Questions on work, energy and power
- A body of mass 10 kg is moving with a speed of 4 m/s. It is brought to rest by a force in 5 seconds. Calculate the work done by the force.
- MHT CET - 2025
- Physics
- work, energy and power
- A force of 10 N is applied to move a body of mass 5 kg over a distance of 3 meters. Find the work done by the force.
- MHT CET - 2025
- Physics
- work, energy and power
A block of certain mass is placed on a rough floor. The coefficients of static and kinetic friction between the block and the floor are 0.4 and 0.25 respectively. A constant horizontal force \( F = 20 \, \text{N} \) acts on it so that the velocity of the block varies with time according to the following graph. The mass of the block is nearly (Take \( g = 10 \, \text{m/s}^2 \)):

- KCET - 2025
- Physics
- work, energy and power
- A 0.5 kg object is moving with a velocity of 10 m/s. What is its kinetic energy?
- MHT CET - 2025
- Physics
- work, energy and power
- A 50 kg person climbs a staircase of height 10 m. Calculate the work done by the person against gravity.
- MHT CET - 2025
- Physics
- work, energy and power
View More Questions
Questions Asked in JEE Main exam
- Let C be the circle of minimum area enclosing the ellipse E: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \) with eccentricity \( \frac{1}{2} \) and foci \( (\pm 2, 0) \). Let PQR be a variable triangle, whose vertex P is on the circle C and the side QR of length 29 is parallel to the major axis and contains the point of intersection of E with the negative y-axis. Then the maximum area of the triangle PQR is:
- JEE Main - 2025
- Coordinate Geometry
- Let circle $C$ be the image of
$$ x^2 + y^2 - 2x + 4y - 4 = 0 $$
in the line
$$ 2x - 3y + 5 = 0 $$
and $A$ be the point on $C$ such that $OA$ is parallel to the x-axis and $A$ lies on the right-hand side of the centre $O$ of $C$.
If $B(\alpha, \beta)$, with $\beta < 4$, lies on $C$ such that the length of the arc $AB$ is $\frac{1}{6}$ of the perimeter of $C$, then $\beta - \sqrt{3}\alpha$ is equal to: 0.01 mole of an organic compound (X) containing 10% hydrogen, on complete combustion, produced 0.9 g H₂O. Molar mass of (X) is ___________g mol\(^{-1}\).
- JEE Main - 2025
- Organic Chemistry
- In the Claisen-Schmidt reaction to prepare dibenzalacetone from 5.3 g benzaldehyde, a total of 3.51 g of product was obtained. The percentage yield in this reaction was _____.
- JEE Main - 2025
- Reaction Mechanisms & Synthesis
- The sum of all local minimum values of the function \( f(x) \) as defined below is:
\[ f(x) = \begin{cases} 1 - 2x & \text{if } x < -1, \\[10pt] \frac{1}{3}(7 + 2|x|) & \text{if } -1 \leq x \leq 2, \\[10pt] \frac{11}{18}(x-4)(x-5) & \text{if } x > 2. \end{cases} \]- JEE Main - 2025
- Functions
View More Questions