The shortest distance between the lines \(x+1=2 y=-12 z\) and \(x=y+2=6 z-6\) is
The shortest distance between the lines \(x+1=2 y=-12 z\) and \(x=y+2=6 z-6\) is
- $\frac{3}{2}$
- 3
- 2
- $\frac{5}{2}$
The Correct Option is C
Approach Solution - 1
The given lines are:
\( x+1 = 2y = -12z \)
and
\( x = y+2 = 6z - 6 \).
The formula for the shortest distance between two skew lines is:
Shortest distance (S.D.) = \(\frac{|(\mathbf{b} - \mathbf{a}) \cdot (\mathbf{p} \times \mathbf{q})|}{|\mathbf{p} \times \mathbf{q}|} \)
Here:
\(\mathbf{a} = (-1, 0, 0), \quad \mathbf{b} = (0, -2, -1), \quad \mathbf{p} = (1, \frac{1}{2}, -\frac{1}{12}), \quad \mathbf{q} = (1, 1, \frac{1}{6}).\)
Step 1: Compute \(\mathbf{p} \times \mathbf{q}\)
The cross product \(\mathbf{p} \times \mathbf{q}\) is given by:
\( \mathbf{p} \times \mathbf{q} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & \frac{1}{2} & -\frac{1}{12} \\ 1 & 1 & \frac{1}{6} \end{vmatrix}. \)
Expanding the determinant:
\( \mathbf{p} \times \mathbf{q} = \mathbf{i} \left( \frac{1}{12} - \left( -\frac{1}{12} \right) \right) - \mathbf{j} \left( \frac{1}{6} - \left( -\frac{1}{12} \right) \right) + \mathbf{k} \left( 1 - \frac{1}{2} \right). \)
Simplifying:
\( \mathbf{p} \times \mathbf{q} = \mathbf{i} \cdot \frac{1}{6} - \mathbf{j} \cdot \frac{1}{4} + \mathbf{k} \cdot 0. \)
So:
\( \mathbf{p} \times \mathbf{q} = \frac{1}{6}\mathbf{i} - \frac{1}{4}\mathbf{j}. \)
Step 2: Compute \(|\mathbf{p} \times \mathbf{q}|\)
The magnitude of \(\mathbf{p} \times \mathbf{q}\) is:
\( |\mathbf{p} \times \mathbf{q}| = \sqrt{\left( \frac{1}{6} \right)^2 + \left( -\frac{1}{4} \right)^2}. \)
Simplifying:
\( |\mathbf{p} \times \mathbf{q}| = \sqrt{\frac{1}{36} + \frac{1}{16}} = \sqrt{\frac{4}{144} + \frac{9}{144}} = \sqrt{\frac{13}{144}} = \frac{\sqrt{13}}{12}. \)
Step 3: Compute \(( \mathbf{b} - \mathbf{a}) \cdot (\mathbf{p} \times \mathbf{q} )\)
The vector \(\mathbf{b} - \mathbf{a}\) is:
\( \mathbf{b} - \mathbf{a} = (0 - (-1), -2 - 0, -1 - 0) = (1, -2, -1). \)
15
The dot product \(( \mathbf{b} - \mathbf{a}) \cdot (\mathbf{p} \times \mathbf{q} )\) is:
\( (1, -2, -1) \cdot \left( \frac{1}{6}, -\frac{1}{4}, 0 \right) = 1 \cdot \frac{1}{6} + (-2) \cdot \left( -\frac{1}{4} \right) + (-1) \cdot 0. \)
Simplifying:
\( (\mathbf{b} - \mathbf{a}) \cdot (\mathbf{p} \times \mathbf{q}) = \frac{1}{6} + \frac{2}{4} + \frac{1}{6} = \frac{1}{6} + \frac{3}{6} = \frac{4}{6} = \frac{2}{3}. \)
Step 4: Compute the shortest distance
Using the formula:
\( \text{S.D.} = \frac{|(\mathbf{b} - \mathbf{a}) \cdot (\mathbf{p} \times \mathbf{q})|}{|\mathbf{p} \times \mathbf{q}|}. \)
Substituting the values:
\( \text{S.D.} = \frac{|\frac{2}{3}|}{\frac{\sqrt{13}}{12}} = \frac{2}{3} \cdot \frac{12}{\sqrt{13}} = \frac{8}{\sqrt{13}}. \)
Finally, rationalizing the denominator gives:
\( \text{S.D.} = \frac{8\sqrt{13}}{13}. \)
Correct Option: 3 (2)
Approach Solution -2
The correct answer is (C) : 2
\(\frac{x+1}{1}=\frac{y}{\frac{1}{2}}=\frac{z}{\frac{-1}{12}} \text{ and } \frac{x}{1}=\frac{y+2}{1}=\frac{z-6}{\frac{1}{6}}\)
\(⇒ \text{Shortest distance}= \frac{(\vec{b}−\vec{a})⋅(\vec{p}\times\vec{q})}{|\vec{p}\times\vec{q}|}\)
\(⇒ \text{S.D.}= (-\hat{i}+2\hat{j}-\hat{k})⋅\frac{(\vec{p}\times\vec{q})}{|\vec{p}\times\vec{q}|}\)
\(\Biggl\{\vec{p}\times\vec{q} \equiv \begin{vmatrix}\hat{i}&\hat{j}&\hat{k}\\1&\frac{1}{2}&\frac{-1}{12}\\1&1&\frac{1}{6}\end{vmatrix}=\frac{1}{6}\hat{i}-\frac{1}{4}\hat{j}+\frac{1}{2}\hat{k} \text{ or } 2\hat{i}-3\hat{j}+6\hat{k} \Biggl\}\)
\(⇒ \text{S.D.}= \frac{(-\hat{i}+2\hat{j}-\hat{k}).(\hat{2i}-3\hat{j}+6\hat{k})}{\sqrt{2^2+3^2+6^2}}\)
Top Questions on Distance between Two Lines
- Let \( P(\alpha, \beta, \gamma) \) be the point on the line \[ \frac{x-1}{2} = \frac{y+1}{-3} = z \] at a distance \( 4\sqrt{14} \) from the point \( (1,-1,0) \) and nearer to the origin. Then the shortest distance between the lines \[ \frac{x-\alpha}{1} = \frac{y-\beta}{2} = \frac{z-\gamma}{3} \quad \text{and} \quad \frac{x+5}{2} = \frac{y-10}{1} = \frac{z-3}{1} \] is equal to
- JEE Main - 2026
- Mathematics
- Distance between Two Lines
- Find the shortest distance between the lines: \[ \frac{x - 1}{2} = \frac{y + 1}{3} = \frac{z}{4}, \quad \frac{x + 2}{1} = \frac{y - 3}{-2} = \frac{z + 1}{2} \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Distance between Two Lines
- The shortest distance (in units) between the lines \(\frac{1 - x}{1} = \frac{2y - 10}{2} = \frac{z + 1}{1}\) and \(\frac{x - 3}{-1} = \frac{y - 5}{1} = \frac{z - 0}{1}\) is:
- CUET (UG) - 2024
- Mathematics
- Distance between Two Lines
- The shortest distance between the lines
\[\frac{x - 3}{2} = \frac{y + 15}{-7} = \frac{z - 9}{5}\]and
\[\frac{x + 1}{2} = \frac{y - 1}{1} = \frac{z - 9}{-3}\] is:- JEE Main - 2024
- Mathematics
- Distance between Two Lines
- If the shortest distance between the lines \[ \frac{x - \lambda}{3} = \frac{y - 2}{-1} = \frac{z - 1}{1} \] and \[ \frac{x + 2}{-3} = \frac{y + 5}{2} = \frac{z - 4}{4} \] is \[ \frac{44}{\sqrt{30}}, \] then the largest possible value of $|\lambda|$ is equal to ________.
- JEE Main - 2024
- Mathematics
- Distance between Two Lines
Questions Asked in JEE Main exam
Let \( \alpha = \dfrac{-1 + i\sqrt{3}}{2} \) and \( \beta = \dfrac{-1 - i\sqrt{3}}{2} \), where \( i = \sqrt{-1} \). If
\[ (7 - 7\alpha + 9\beta)^{20} + (9 + 7\alpha - 7\beta)^{20} + (-7 + 9\alpha + 7\beta)^{20} + (14 + 7\alpha + 7\beta)^{20} = m^{10}, \] then the value of \( m \) is ___________.- JEE Main - 2026
- Complex Numbers and Quadratic Equations
- The work functions of two metals ($M_A$ and $M_B$) are in the 1 : 2 ratio. When these metals are exposed to photons of energy 6 eV, the kinetic energy of liberated electrons of $M_A$ : $M_B$ is in the ratio of 2.642 : 1. The work functions (in eV) of $M_A$ and $M_B$ are respectively.
- JEE Main - 2026
- Dual nature of matter
- 10 mole of an ideal gas is undergoing the process shown in the figure. The heat involved in the process from \( P_1 \) to \( P_2 \) is \( \alpha \) Joule \((P_1 = 21.7 \text{ Pa}, P_2 = 30 \text{ Pa}, C_v = 21 \text{ J/K mol}, R = 8.3 \text{ J/mol K})\). The value of \( \alpha \) is ________.
- JEE Main - 2026
- Thermodynamics
- The system of linear equations
$x + y + z = 6$
$2x + 5y + az = 36$
$x + 2y + 3z = b$
has- JEE Main - 2026
- Matrices and Determinants
- The displacement of a particle executing simple harmonic motion with time period \(T\) is expressed as \[ x(t)=A\sin\omega t, \] where \(A\) is the amplitude of oscillation. If the maximum value of the potential energy of the oscillator is found at \[ t=\frac{T}{2\beta}, \] then the value of \(\beta\) is ________.
- JEE Main - 2026
- Waves and Oscillations
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
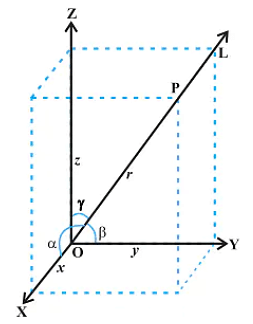
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.