The shortest distance between the lines $\frac{x-5}{1}=\frac{y-2}{2}=\frac{z-4}{-3}$ and $\frac{x+3}{1}=\frac{y+5}{4}=\frac{z-1}{-5}$ is
- $7 \sqrt{3}$
- $6 \sqrt{3}$
- $4 \sqrt{3}$
- $5 \sqrt{3}$
The Correct Option is B
Approach Solution - 1
The correct answer is option (B) : \(6 \sqrt{3}\)
Shortest distance between two lines
\(\frac{x-x_1}{a_1} = \frac{y-y_1}{a_2} = \frac{z-z_1}{a_3}\) and \(\frac{x-x_2}{b_1} = \frac{y-y_2}{b_2} = \frac{z-z_2}{b_3}\) is given as
\(= \frac{\begin{vmatrix} x_1-x_2 & y_1-y_2 & z_1-z_2\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix}}{\sqrt{(a_1b_3-a_3b_2)^2+(a_1b_3-a_3b_1)^2+(a_1b_2-a_2b_1)^2}}\)
\(= \frac{\begin{vmatrix} 5-(3) & 2-(-5) & 4-1\\ 1 & 2 & -3\\ 1 & 4 & -5 \end{vmatrix}}{\sqrt{(-10+12)^2+(-5+3)^2+(4-2)^2}}\)
\(= \frac{\begin{vmatrix} 8 & 7 & 3\\ 1 & 2 & -3\\ 1 & 4 & -5 \end{vmatrix}}{\sqrt{(2)^2+(-2)^2+(2)^2}}\)
\(= \frac{\begin{vmatrix} 8(-10+12)-7(-5+3)+3(4-2)\end{vmatrix}}{\sqrt{4+4+4}}\)
\(= \frac{\begin{vmatrix} 16+14+6\end{vmatrix}}{\sqrt{12}}\)
\(= \frac{36}{\sqrt{12}} = \frac{36}{2\sqrt{3}}\)
\(= \frac{18}{\sqrt{3}} = 6\sqrt{3}\)
Approach Solution -2
Step 1: Shortest distance formula between skew lines: \[ d = \frac{|(a_1 b_2 - a_2 b_1) + (a_2 b_3 - a_3 b_2) + (a_3 b_1 - a_1 b_3)|} {\sqrt{(a_1 - a_2)^2 + (b_1 - b_2)^2 + (c_1 - c_2)^2}} \]
Step 2: Substituting values, \[ d = \frac{8(-10 + 12) - 7(-5 + 3) + 3(4 - 2)}{\sqrt{4 + 4 + 4}} \] \[ = \frac{16 + 14 + 6}{\sqrt{12}} = \frac{36}{\sqrt{12}} = \frac{36}{2\sqrt{3}} \] \[ = \frac{18}{\sqrt{3}} = 6\sqrt{3} \]
Top Questions on Distance between Two Lines
- Let \( P(\alpha, \beta, \gamma) \) be the point on the line \[ \frac{x-1}{2} = \frac{y+1}{-3} = z \] at a distance \( 4\sqrt{14} \) from the point \( (1,-1,0) \) and nearer to the origin. Then the shortest distance between the lines \[ \frac{x-\alpha}{1} = \frac{y-\beta}{2} = \frac{z-\gamma}{3} \quad \text{and} \quad \frac{x+5}{2} = \frac{y-10}{1} = \frac{z-3}{1} \] is equal to
- JEE Main - 2026
- Mathematics
- Distance between Two Lines
- Find the shortest distance between the lines: \[ \frac{x - 1}{2} = \frac{y + 1}{3} = \frac{z}{4}, \quad \frac{x + 2}{1} = \frac{y - 3}{-2} = \frac{z + 1}{2} \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Distance between Two Lines
- The shortest distance (in units) between the lines \(\frac{1 - x}{1} = \frac{2y - 10}{2} = \frac{z + 1}{1}\) and \(\frac{x - 3}{-1} = \frac{y - 5}{1} = \frac{z - 0}{1}\) is:
- CUET (UG) - 2024
- Mathematics
- Distance between Two Lines
- The shortest distance between the lines
\[\frac{x - 3}{2} = \frac{y + 15}{-7} = \frac{z - 9}{5}\]and
\[\frac{x + 1}{2} = \frac{y - 1}{1} = \frac{z - 9}{-3}\] is:- JEE Main - 2024
- Mathematics
- Distance between Two Lines
- If the shortest distance between the lines \[ \frac{x - \lambda}{3} = \frac{y - 2}{-1} = \frac{z - 1}{1} \] and \[ \frac{x + 2}{-3} = \frac{y + 5}{2} = \frac{z - 4}{4} \] is \[ \frac{44}{\sqrt{30}}, \] then the largest possible value of $|\lambda|$ is equal to ________.
- JEE Main - 2024
- Mathematics
- Distance between Two Lines
Questions Asked in JEE Main exam
- In a microscope of tube length $10\,\text{cm}$ two convex lenses are arranged with focal lengths $2\,\text{cm}$ and $5\,\text{cm}$. Total magnification obtained with this system for normal adjustment is $(5)^k$. The value of $k$ is ___.
- JEE Main - 2026
- Optical Instruments
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
- Let \( ABC \) be an equilateral triangle with orthocenter at the origin and the side \( BC \) lying on the line \( x+2\sqrt{2}\,y=4 \). If the coordinates of the vertex \( A \) are \( (\alpha,\beta) \), then the greatest integer less than or equal to \( |\alpha+\sqrt{2}\beta| \) is:
- JEE Main - 2026
- Coordinate Geometry
- Three charges $+2q$, $+3q$ and $-4q$ are situated at $(0,-3a)$, $(2a,0)$ and $(-2a,0)$ respectively in the $x$-$y$ plane. The resultant dipole moment about origin is ___.
- JEE Main - 2026
- Electromagnetic waves
Let \( \alpha = \dfrac{-1 + i\sqrt{3}}{2} \) and \( \beta = \dfrac{-1 - i\sqrt{3}}{2} \), where \( i = \sqrt{-1} \). If
\[ (7 - 7\alpha + 9\beta)^{20} + (9 + 7\alpha - 7\beta)^{20} + (-7 + 9\alpha + 7\beta)^{20} + (14 + 7\alpha + 7\beta)^{20} = m^{10}, \] then the value of \( m \) is ___________.- JEE Main - 2026
- Complex Numbers and Quadratic Equations
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
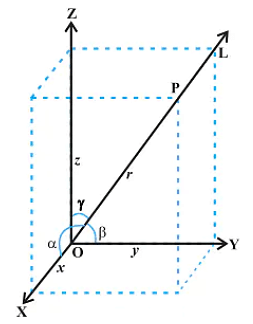
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.