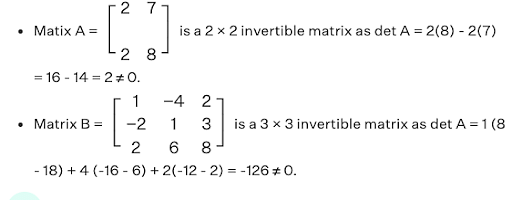Question:
The inverse of the matrix $\begin{bmatrix}
{5}&{-2}\\
{3}&{1}\\
\end{bmatrix}$ is is
The inverse of the matrix $\begin{bmatrix}
{5}&{-2}\\
{3}&{1}\\
\end{bmatrix}$ is is
Updated On: May 17, 2024
- $\frac {1}{11}\begin{bmatrix} {1}&{2}\\ {-3}&{5}\\ \end{bmatrix} $
- $\begin{bmatrix} {1}&{2}\\ {-3}&{5}\\ \end{bmatrix} $
- $\frac {1}{13}\begin{bmatrix} {-2}&{5}\\ {1}&{3}\\ \end{bmatrix} $
- $\begin{bmatrix} {1}&{3}\\ {-2}&{5}\\ \end{bmatrix} $
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Let $A=\begin{bmatrix}5 & -2 \\ 3 & 1\end{bmatrix}$
$|A|=5+6=11$
and $adj\, A=\begin{bmatrix}1 & 2 \\ -3 & 5\end{bmatrix}$
$A^{-1}=\frac{1}{|A|}$ (adj A) $=\frac{1}{11}\begin{bmatrix}1 & 2 \\ -3 & 5\end{bmatrix}$
Was this answer helpful?
0
0
Top Questions on Invertible Matrices
- If A is a non-identity invertible symmetric matrix, then \(A^{-1}\) is:
- CUET (UG) - 2023
- Mathematics
- Invertible Matrices
- The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- Which of the following matrices can NOT be obtained from the matrix \(\begin{bmatrix} -1 &2 \\ 1 & -1 \end{bmatrix}\) by a single elementary row operation?
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- If A and B are invertible matrices then which of the following is not correct ?
- KCET - 2021
- Mathematics
- Invertible Matrices
- The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
- KCET - 2019
- Mathematics
- Invertible Matrices
View More Questions
Questions Asked in KCET exam
- If the number of terms in the binomial expansion of \((2x + 3)^n\) is 22, then the value of \(n\) is:
- KCET - 2025
- Binomial theorem
- Ethyl alcohol is heated with concentrated sulphuric acid at 413 K (140°C). The major product formed is
- KCET - 2025
- Organic Chemistry
- A body of mass 0.25 kg travels along a straight line from \( x = 0 \) to \( x = 2 \, \text{m} \) with a speed \( v = k x^2 \) where \( k = 2 \, \text{m}^{-1} \). The work done by the net force during this displacement is
- KCET - 2025
- Elastic and inelastic collisions
- A square loop of side 2 m lies in the Y-Z plane in a region having a magnetic field \(\mathbf{B} = (5 \hat{i} - 3 \hat{j} - 4 \hat{k}) \, \text{T}\). The magnitude of magnetic flux through the square loop is
- KCET - 2025
- Magnetic Field
- A random experiment has five outcomes \(w_1, w_2, w_3, w_4, w_5\). The probabilities of the occurrence of the outcomes \(w_1, w_2, w_4, w_5\) are respectively \( \frac{1}{6}, a, b, \frac{1}{12} \) such that \(12a + 12b - 1 = 0\). Then the probabilities of occurrence of the outcome \(w_3\) is:
- KCET - 2025
- Probability
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.