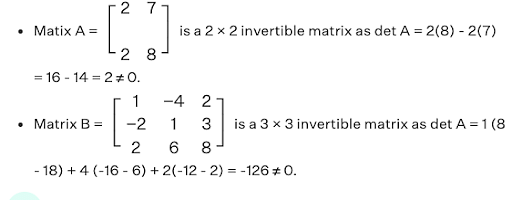Question:
The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
The inverse of the matrix $\begin{bmatrix}2&5&0\\ 0&1&1\\ -1&0&3\end{bmatrix} $ is
Updated On: Apr 8, 2024
- $\begin{bmatrix}3&-15&5\\ -1&6&-2\\ 1&-5&2\end{bmatrix}$
- $\begin{bmatrix}3&-1&1\\ -15&6&-5\\ 5&-2&2\end{bmatrix}$
- $\begin{bmatrix}3&-15&5\\ -1&6&-2\\ 1&-5&-2\end{bmatrix}$
- $\begin{bmatrix}3&-5&5\\ -1&-6&-2\\ 1&-5&2\end{bmatrix}$
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
$Let A=\left[\begin{matrix}2&5&0\\ 0&1&1\\ -1&0&3\end{matrix}\right]$
$\left|A\right|=2\left(3-0\right)-5\left(0+1\right)$
$ = 6 - 5 = 1$
$\therefore\, \left|A\right|=1$
$adj \, A=\left[\begin{matrix}3&-1&1\\ -15&6&-5\\ 5&-2&2\end{matrix}\right]^{T}=\left[\begin{matrix}3&-15&5\\ -1&6&-2\\ 1&-5&2\end{matrix}\right]$
$A^{-1}=\frac{adj\, A}{\left|A\right|}=\left[\begin{matrix}3&-15&5\\ -1&6&-2\\ 1&-5&2\end{matrix}\right]$
$\left|A\right|=2\left(3-0\right)-5\left(0+1\right)$
$ = 6 - 5 = 1$
$\therefore\, \left|A\right|=1$
$adj \, A=\left[\begin{matrix}3&-1&1\\ -15&6&-5\\ 5&-2&2\end{matrix}\right]^{T}=\left[\begin{matrix}3&-15&5\\ -1&6&-2\\ 1&-5&2\end{matrix}\right]$
$A^{-1}=\frac{adj\, A}{\left|A\right|}=\left[\begin{matrix}3&-15&5\\ -1&6&-2\\ 1&-5&2\end{matrix}\right]$
Was this answer helpful?
0
0
Top Questions on Invertible Matrices
- If A is a non-identity invertible symmetric matrix, then \(A^{-1}\) is:
- CUET (UG) - 2023
- Mathematics
- Invertible Matrices
- The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- Which of the following matrices can NOT be obtained from the matrix \(\begin{bmatrix} -1 &2 \\ 1 & -1 \end{bmatrix}\) by a single elementary row operation?
- JEE Main - 2022
- Mathematics
- Invertible Matrices
- If A and B are invertible matrices then which of the following is not correct ?
- KCET - 2021
- Mathematics
- Invertible Matrices
- If $A = \begin{bmatrix}2&-2\\ -2&2\end{bmatrix}$ then $A^n = 2^k A,$ where k =
- KCET - 2018
- Mathematics
- Invertible Matrices
View More Questions
Questions Asked in KCET exam
- Ten identical cells each emf 2V and internal resistance 1Ω are connected in series with two cells wrongly connected. A resistor of 10Ω is connected to the combination. What is the current through the resistor?
- KCET - 2023
- Cells in Series and in Parallel
- The speed of sound in an ideal gas at a given temperature T is v. The rms speed of gas molecules at that temperature is vrms. The ratio of the velocities v and vrms for helium and oxygen gases are X and X' respectively. Then \(\frac{X}{X'}\) is equal to
- KCET - 2023
- Thermodynamics
- If \(p(\frac{1}{q}+\frac{1}{r}),q(\frac{1}{r}+\frac{1}{p}),r(\frac{1}{p}+\frac{1}{q})\) are in A.P., then p, q, r
- KCET - 2023
- Arithmetic Progression
- A stretched wire of a material whose Young's modulus Y = 2 × 1011 Nm-2 has Poisson's ratio of 0.25. Its lateral strain εl = 10-3. The elastic energy density of the wire is
- KCET - 2023
- mechanical properties of solids
- A metallic rod of length 1 m held along east-west direction is allowed to fall down freely. Given horizontal component of earth’s magnetic field BH = 3 × 10-5 T. The emf induced in the rod at an instant t = 2s after it is released is ( Take g = 10 ms-2 )
- KCET - 2023
- Faradays laws of induction
View More Questions
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.
