The combined equation of the two lines $a x+b y+c=0$ and $a^{\prime} x+b^{\prime} y+c^{\prime}=0$ can be written as $(a x+b y+c)\left(a^{\prime} x+b^{\prime} y+c^{\prime}\right)=0$
The equation of the angle bisectors of the lines represented by the equation $2 x^2+x y-3 y^2=0$ is
The equation of the angle bisectors of the lines represented by the equation $2 x^2+x y-3 y^2=0$ is
- $3 x^2+5 x y+2 y^2=0$
- $x^2-y^2-10 x y=0$
- $3 x^2+x y-2 y^2=0$
- $x^2-y^2+10 x y=0$
The Correct Option is B
Solution and Explanation
Here
Equation will become
Top Questions on measurement of angles
- The angle of elevation of a cloud $C$ from a point $P , 200 m$ above a still lake is $30^{\circ} .$ If the angle of depression of the image of $C$ in the lake from the point $P$ is $60^{\circ}$, then $P C$ (in $m$ ) is equal to :
- JEE Main - 2020
- Mathematics
- measurement of angles
- The approximate value of $\sin \, 31^{\circ}$ is
- WBJEE - 2018
- Mathematics
- measurement of angles
- The acute angle between the hour hand and minute hand of a clock when the time is $5\, hours$ and $40\, minute$ is
- COMEDK UGET - 2008
- Mathematics
- measurement of angles
- The angles $A, B$ and $C$ of a triangle $ABC$ are in A.P. If $b : c =\sqrt {3} : \sqrt {2}$ then the angle $A$ is
- KCET - 2008
- Mathematics
- measurement of angles
- The angle between two hands of a clock at quarter past one is
- Mathematics
- measurement of angles
Questions Asked in JEE Main exam
- A convex lens of focal length 40 cm forms an image of an extended source of light on a photo-electric cell. A current \( I \) is produced. The lens is replaced by another convex lens having the same diameter but focal length 20 cm. The photoelectric current now is:
- JEE Main - 2024
- Dual nature of matter
- For a sparingly soluble salt \( \text{AB}_2 \), the equilibrium concentrations of \( \text{A}^{2+} \) ions and \( \text{B}^- \) ions are \( 1.2 \times 10^{-4} \, \text{M} \) and \( 0.24 \times 10^{-3} \, \text{M} \), respectively. The solubility product of \( \text{AB}_2 \) is:
- JEE Main - 2024
- Method of Preparation of Diazoniun Salts
The portion of the line \( 4x + 5y = 20 \) in the first quadrant is trisected by the lines \( L_1 \) and \( L_2 \) passing through the origin. The tangent of an angle between the lines \( L_1 \) and \( L_2 \) is:
- JEE Main - 2024
- Tangents and Normals
- Let \[ \vec{a} = 2\hat{i} + \alpha \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} + \hat{k}, \quad \vec{c} = \beta \hat{j} - \hat{k}, \] where \( \alpha \) and \( \beta \) are integers and \( \alpha \beta = -6 \). Let the values of the ordered pair \( (\alpha, \beta) \) for which the area of the parallelogram of diagonals \( \vec{a} + \vec{b} \) and \( \vec{b} + \vec{c} \) is \( \frac{\sqrt{21}}{2} \), be \( (\alpha_1, \beta_1) \) and \( (\alpha_2, \beta_2) \). Then \( \alpha_1^2 + \beta_1^2 - \alpha_2 \beta_2 \) is equal to:
- JEE Main - 2024
- Vectors
- The molecular formula of second homologue in the homologous series of monocarboxylic acid is
- JEE Main - 2024
- Aldehydes, Ketones and Carboxylic Acids
Concepts Used:
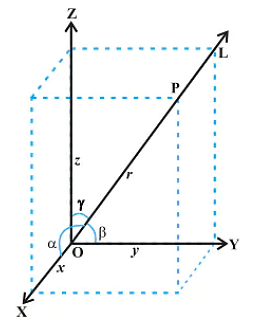
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.
