Question

The area of the region satisfying the inequalities \(|x|-y≤1,y≥0\) and \(y≤1\) is

Answer 1

The graph of \(|x|-y≤1,y≥0\) and \(y≤1\) is as follows: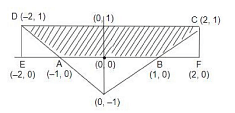
 

We are given the decomposition: \[ \text{Area of } ABCD = \text{Area of } EFCD - \text{Area of } EAD - \text{Area of } BFC \]

Step-by-step calculation:

Using the formula: \[ \text{Area} = EF \times FC - \frac{1}{2} \times EA \times ED - \frac{1}{2} \times BF \times FC \]

Substitute the values: \[ = 4 \times 1 - \frac{1}{2} \times 1 \times 1 - \frac{1}{2} \times 1 \times 1 \]

Simplifying: \[ = 4 - \frac{1}{2} - \frac{1}{2} = 4 - 1 = \boxed{3} \]

✅ Final Answer: \( \boxed{3} \) square units

Answer 2

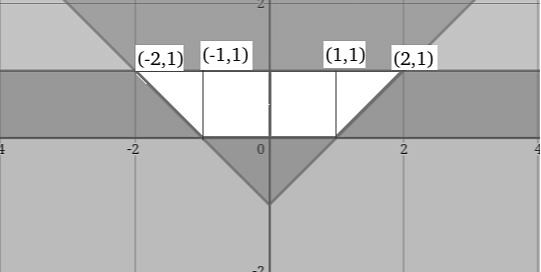
We are given the region bounded by the inequalities:

\[ |x| - y \leq 1, \quad y \geq 0, \quad y \leq 1 \]

Step 1: Rewrite the first inequality:
\[ |x| - y \leq 1 \Rightarrow y \geq |x| - 1 \] So the region lies above the curve \( y = |x| - 1 \), and between \( y = 0 \) and \( y = 1 \).

Step 2: Analyze the region:
- The graph of \( y = |x| - 1 \) is a "V"-shaped graph shifted down by 1.
- The region of interest lies between \( y = |x| - 1 \) and \( y = 1 \), for \( y \geq 0 \).
- The intersection points occur where \( |x| - 1 = 0 \Rightarrow |x| = 1 \Rightarrow x = \pm 1 \).
- So the base of the region goes from \( x = -2 \) to \( x = 2 \) at \( y = 1 \).

Step 3: Break the region into geometric shapes:
- A central rectangle of width 2 (from \( x = -1 \) to \( x = 1 \)) and height 1.
- Two right triangles on either side, each of base 1 and height 1.

Total Area:
\[ \text{Area} = \text{Area of rectangle} + 2 \times \text{Area of triangle} \] \[ = (1 \times 2) + 2 \times \left(\frac{1}{2} \times 1 \times 1\right) = 2 + 1 = \boxed{3} \]

Final Answer: \( \boxed{3} \)