Question:
Plane P3 is passing through (1,1,1) and line of intersection of P1 and P2 where \(P_{1}: 2x - y + z = 5\) and \(P_{2}: x + 3y + 2z + 2 = 0\). Then distance of (1,1,10) from P3 is:
Plane P3 is passing through (1,1,1) and line of intersection of P1 and P2 where \(P_{1}: 2x - y + z = 5\) and \(P_{2}: x + 3y + 2z + 2 = 0\). Then distance of (1,1,10) from P3 is:
Updated On: Feb 14, 2025
- \(\frac{53}{85}\)
\(\sqrt{85}\)
- \(\frac{52}{\sqrt{85}}\)
- 53
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct option is (C): \(\frac{52}{\sqrt{85}}\)
Was this answer helpful?
0
0
Top Questions on Three Dimensional Geometry
- If A(2,1,-1), B(6,-3,2), C(-3,12,4) are the vertices of a triangle ABC and the equation of the plane containing the triangle ABC is $53x+by+cz+d=0$, then $\frac{d}{b+c}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If $(\alpha, \beta, \gamma)$ is the foot of the perpendicular drawn from a point $(-1,2,-1)$ to the line joining the points $(2,-1,1)$ and $(1,1,-2)$, then $\alpha+\beta+\gamma=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If m:n is the ratio in which the point $\left(\frac{8}{5}, \frac{1}{5}, \frac{8}{5}\right)$ divides the line segment joining the points (2,p,2) and (p,-2,p) where p is an integer then $\frac{3m+n}{3n}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- Let $\pi_1$ be the plane determined by the vectors $\hat{i}+\hat{j}, \hat{i}+\hat{k}$ and $\pi_2$ be the plane determined by the vectors $\hat{j}-\hat{k}, \hat{k}-\hat{i}$. Let $\vec{a}$ be a non-zero vector parallel to the line of intersection of the planes $\pi_1$ and $\pi_2$. If $\vec{b} = \hat{i}+\hat{j}-\hat{k}$ then the angle between the vectors $\vec{a}$ and $\vec{b}$ is
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
Show that the following lines intersect. Also, find their point of intersection:
Line 1: \[ \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} \]
Line 2: \[ \frac{x - 4}{5} = \frac{y - 1}{2} = z \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
View More Questions
Questions Asked in JEE Main exam
- A group 15 element forms \( d\pi - d\pi \) bond with transition metals. It also forms a hydride, which is the strongest base among the hydrides of other group members that form \( d\pi - d\pi \) bonds. The atomic number of the element is ________________________.
- JEE Main - 2025
- Chemical bonding and molecular structure
- The value of \( (\sin 70^\circ)(\cot 10^\circ \cot 70^\circ - 1) \) is:
- JEE Main - 2025
- Trigonometric Identities
- Match List-I with List-II.

- JEE Main - 2025
- Dimensional analysis
Nature of compounds TeO₂ and TeH₂ is___________ and ______________respectively.
- JEE Main - 2025
- Inorganic chemistry
- Let \( A = [a_{ij}] \) be a matrix of order 3 \(\times\) 3, with \(a_{ij} = (\sqrt{2})^{i+j}\). If the sum of all the elements in the third row of \( A^2 \) is \( \alpha + \beta\sqrt{2} \), where \(\alpha, \beta \in \mathbb{Z}\), then \(\alpha + \beta\) is equal to:
- JEE Main - 2025
- Matrices and Determinants
View More Questions
Concepts Used:
Distance of a Point from a Plane
The shortest perpendicular distance from the point to the given plane is the distance between point and plane. In simple terms, the shortest distance from a point to a plane is the length of the perpendicular parallel to the normal vector dropped from the particular point to the particular plane. Let's see the formula for the distance between point and plane.
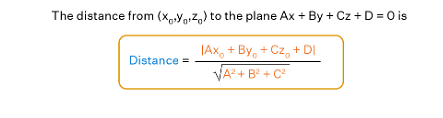
Read More: Distance Between Two Points