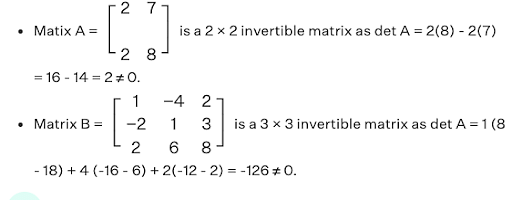Matrices A and B will be inverse of each other only if
Matrices A and B will be inverse of each other only if
AB = BA
AB = BA = 0
AB = 0, BA = I
AB = BA = I
The Correct Option is D
Solution and Explanation
We know that if A is a square matrix of order m, and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is said to be the inverse of A.
In this case, it is clear that A is the inverse of B.
Thus, matrices A and B will be inverses of each other only if AB = BA = I.
Top Questions on Matrices
- If $A$ and $B$ are two square matrices each of order 3 with $|A| = 3$ and $|B| = 5$, then $|2AB|$ is:
- If \( \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} \) is a scalar matrix, then \( x^y \) is equal to:
- If $M$ and $N$ are square matrices of order 3 such that $\det(M) = m$ and $MN = mI$, then $\det(N)$ is equal to :
- Let \( A = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} \). The determinant of \( A^3 \) is:
- If \( A = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} \), find the determinant of \( A^2 \).
Questions Asked in CBSE CLASS XII exam
- Enumerate any two myths related to food items with their respective facts.
- CBSE CLASS XII - 2025
- Food and Nutrition
- You are provided with a large number of 1 \(\mu\text{F}\) identical capacitors and a power supply of 1200 V. The dielectric medium used in each capacitor can withstand up to 200 V only. Find the minimum number of capacitors and their arrangement required to build a capacitor system of equivalent capacitance of 2 \(\mu\text{F}\) for use with this supply.
- CBSE CLASS XII - 2025
- Combination of capacitors
- A parallel plate capacitor with plate area \( A \) and plate separation \( d \) has a capacitance \( C_0 \). A slab of dielectric constant \( K \) having area \( A \) and thickness \( \left(\frac{d}{4}\right) \) is inserted in the capacitor, parallel to the plates. Find the new value of its capacitance.
- CBSE CLASS XII - 2025
- capacitor with a dielectric
- An electric dipole of dipole moment \( 1.0 \times 10^{-12} \ \text{Cm} \) lies along the x-axis. An electric field of magnitude \( 2.0 \times 10^4 \ \text{NC}^{-1} \) is switched on at an instant in the region. The unit vector along the electric field is \( \frac{\sqrt{3}}{2} \hat{i} + \frac{1}{2} \hat{j} \). The magnitude of the torque acting on the dipole at that instant is:
- The maximum value of \(Z = 3x + 4y\) subject to the constraints \(x + y \leq 1\), \(x \geq 0\), \(y \geq 0\) is:
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Linear Programming
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.