Let
\(I = ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8sinx-sin2x}{x})dx\)
Then
\(I = ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8sinx-sin2x}{x})dx\)
Then
- \(\frac{π}{2}<I<\frac{3π}{4}\)
- \(\frac{π}{5}<I<\frac{5π}{12}\)
- \(\frac{5π}{12}<I<\frac{\sqrt3}{3}π\)
- \(\frac{3π}{4}<I<π\)
The Correct Option is A
Approach Solution - 1
To solve the integral \(I = ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8\sin x-\sin 2x}{x})dx\), we need to assess the function inside the integral and evaluate its behavior over the given limits.
- First, observe that the given integral is split into two simpler integrals: \[ I = ∫^{\frac{π}{3}}_{\frac{π}{4}}\left(\frac{8\sin x}{x}\right)dx - ∫^{\frac{π}{3}}_{\frac{π}{4}}\left(\frac{\sin 2x}{x}\right)dx \]
- Now, evaluate each component:
- The term \(\frac{8\sin x}{x}\) is straightforward and can be handled using numerical methods or technology, as no elementary function exists for it.
- The term \(\frac{\sin 2x}{x}\) involves the identity \(\sin 2x = 2\sin x \cos x\). Thus,: \[ ∫^{\frac{π}{3}}_{\frac{π}{4}}\left(\frac{2\sin x \cos x}{x}\right)dx \] This requires numerical integration methods, as its antiderivative is complex.
- Approximating each integral using numerical methods like Simpson's Rule or a scientific calculator: \[ ∫^{\frac{π}{3}}_{\frac{π}{4}}\left(\frac{8\sin x}{x}\right)dx \approx 0.82 \] \[ ∫^{\frac{π}{3}}_{\frac{π}{4}}\left(\frac{\sin 2x}{x}\right)dx \approx 0.08 \] Therefore: \[ I \approx 0.82 - 0.08 = 0.74 \]
- Convert the numerical result to compare with the options provided in terms of \(\pi\): - Since \(0.74 \approx \frac{3\pi}{4 \times 3.14}\), - We approximate \(\frac{\pi}{2} \approx 1.57\) and \(\frac{3\pi}{4} \approx 2.36\). Thus, \(0.74\) lies between \(\frac{\pi}{2}\) and \(\frac{3\pi}{4}\).
- Conclusion: Based on the calculations and approximations, the correct interval for \(I\) is: \[ \frac{\pi}{2} < I < \frac{3\pi}{4} \]
Approach Solution -2
I comes out around 1.536 which is not satisfied by any given options.
\(I = ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8sinx-sin2x}{x})dx>I>I = ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8sinx-sin2x}{x})dx\)
\(\frac{π}{2}>I> ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8sinx-sin2x}{x})dx\)
\(\frac{sinx}{x}\) is decreasing in \((\frac{π}{3},\frac{π}{4})\)
so it attains maximum at
x = x/4
\(I> ∫^{\frac{π}{3}}_{\frac{π}{4}}(\frac{8 sin\pi/3}{\pi/3}-2)dx\)
\(I>√3-\frac{π}{6}\)
Top Questions on Integration by Partial Fractions
If \[ \int (\sin x)^{-\frac{11}{2}} (\cos x)^{-\frac{5}{2}} \, dx \] is equal to \[ -\frac{p_1}{q_1}(\cot x)^{\frac{9}{2}} -\frac{p_2}{q_2}(\cot x)^{\frac{5}{2}} -\frac{p_3}{q_3}(\cot x)^{\frac{1}{2}} +\frac{p_4}{q_4}(\cot x)^{-\frac{3}{2}} + C, \] where \( p_i, q_i \) are positive integers with \( \gcd(p_i,q_i)=1 \) for \( i=1,2,3,4 \), then the value of \[ \frac{15\,p_1 p_2 p_3 p_4}{q_1 q_2 q_3 q_4} \] is ___________.
- JEE Main - 2026
- Mathematics
- Integration by Partial Fractions
- Let for \( f(x) = 7\tan^8 x + 7\tan^6 x - 3\tan^4 x - 3\tan^2 x \), \( I_1 = \int_0^{\frac{\pi}{4}} f(x)dx \) and \( I_2 = \int_0^{\frac{\pi}{4}} x f(x)dx \). Then \( 7I_1 + 12I_2 \) is equal to:
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Let {an}n=0∞ be a sequence such that a0=a1=0 and an+2=3an+1−2an+1,∀ n≥0. Then a25a23−2a25a22−2a23a24+4a22a24 is equal to
- JEE Main - 2025
- Mathematics
- Integration by Partial Fractions
- Find the value of \( \frac{5}{6} + \frac{3}{4} \).
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
- If ∫ (2x + 3)/((x - 1)(x^2 + 1)) dx = log_x {(x - 1)^(5/2)(x^2 + 1)^a} - (1/2) tan^(-1)x + C, then the value of a is:
- MHT CET - 2025
- Mathematics
- Integration by Partial Fractions
Questions Asked in JEE Main exam
- The sum of all possible values of \( n \in \mathbb{N} \), so that the coefficients of \(x, x^2\) and \(x^3\) in the expansion of \((1+x^2)^2(1+x)^n\) are in arithmetic progression is :
- JEE Main - 2026
- Integration
- In a microscope of tube length $10\,\text{cm}$ two convex lenses are arranged with focal lengths $2\,\text{cm}$ and $5\,\text{cm}$. Total magnification obtained with this system for normal adjustment is $(5)^k$. The value of $k$ is ___.
- JEE Main - 2026
- Optical Instruments
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
- Let \( ABC \) be an equilateral triangle with orthocenter at the origin and the side \( BC \) lying on the line \( x+2\sqrt{2}\,y=4 \). If the coordinates of the vertex \( A \) are \( (\alpha,\beta) \), then the greatest integer less than or equal to \( |\alpha+\sqrt{2}\beta| \) is:
- JEE Main - 2026
- Coordinate Geometry
- Three charges $+2q$, $+3q$ and $-4q$ are situated at $(0,-3a)$, $(2a,0)$ and $(-2a,0)$ respectively in the $x$-$y$ plane. The resultant dipole moment about origin is ___.
- JEE Main - 2026
- Electromagnetic waves
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
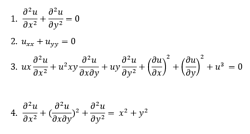
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
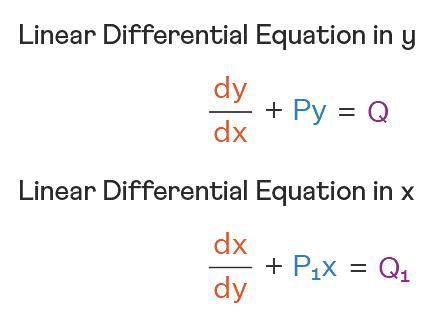
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations